/Szkoła średnia/Zadania maturalne/Matura 2024

Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 4 czerwca 2024 Czas pracy: 180 minut

Zadanie 1
(2 pkt)

W chwili początkowej (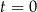t = 0 ) zainicjowano pewną reakcję chemiczną, w której brał udział związek 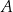A . W wyniku tej reakcji masa 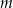m związku 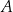A zmieniała się w czasie zgodnie z zależnością

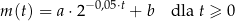
− 0,05⋅t m (t) = a⋅2 + b dla t ≥ 0

gdzie:

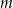  • m – masa związku 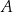A wyrażona w gramach,

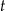  • t – czas wyrażony w sekundach (liczony od chwili t = 0 ),

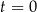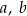  • a, b – współczynniki liczbowe.

Masa początkowa związku 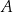A (tj. masa w chwili 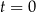t = 0 ) była równa 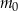m 0 gramów. Po osiągnięciu stanu równowagi (tj. gdy 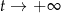t → + ∞ ) masa tego związku była równa 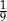19 jego masy początkowej (zobacz rysunek).

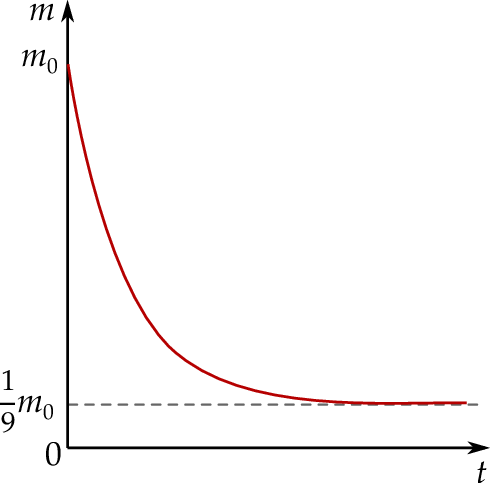
ZINFO-FIGURE

Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało 87,5% masy początkowej tego związku.

Zadanie 2
(2 pkt)

Oblicz granicę

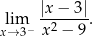
|x− 3| lim -------. x→ 3− x2 − 9

Zadanie 3
(3 pkt)

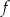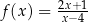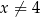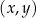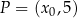Funkcja f jest określona wzorem 2x+1- f(x ) = x− 4 dla każdej liczby rzeczywistej x ⁄= 4 . W kartezjańskim układzie współrzędnych (x,y) punkt P = (x0,5) należy do wykresu funkcji 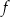f . Oblicz 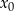x0 oraz wyznacz równanie stycznej do wykresu funkcji 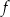f w punkcie P .

Zadanie 4
(3 pkt)

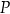Doświadczenie losowe polega na dziesięciokrotnym rzucie symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu losowym orzeł wypadł dokładnie trzy razy z rzędu, jeśli wiadomo, że wypadł dokładnie trzy razy.

Zadanie 5
(3 pkt)

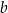Wykaż, że dla każdej liczby dodatniej a i każdej liczby dodatniej b takich, że 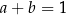a+ b = 1 , prawdziwa jest nierówność

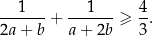
1 1 4 ------+ -------≥ -. 2a+ b a+ 2b 3

Zadanie 6
(3 pkt)

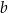Długości podstaw trapezu równoramiennego są równe a oraz b , przy czym 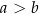a > b . W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od a⋅b .

Zadanie 7
(4 pkt)

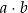Nieskończony ciąg geometryczny 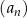(an) jest określony dla każdej liczby naturalnej 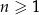n ≥ 1 . Suma wszystkich wyrazów ciągu 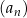(an) o numerach nieparzystych jest równa 16, tj.

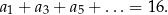
a1 + a3 + a5 + ...= 16.

Ponadto 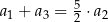a1 + a3 = 52 ⋅a2 . Wyznacz wzór ogólny na n–ty wyraz ciągu (an) .

Zadanie 8
(4 pkt)

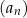W okrąg o promieniu 4 wpisano trójkąt 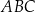ABC . Długość boku 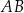AB jest równa 6. Bok 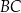BC ma długość 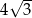4√ 3- i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku 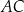AC trójkąta ABC .

Zadanie 9
(4 pkt)

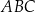Rozwiąż równanie 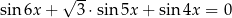√ -- sin 6x + 3 ⋅sin5x + sin 4x = 0 .

Zadanie 10
(4 pkt)

Długość krawędzi podstawy graniastosłupa prawidłowego trójkątnego jest równa a . Sinus kąta między przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka 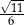√ -- --11 6 . Wyznacz pole powierzchni całkowitej tego graniastosłupa.

Zadanie 11
(6 pkt)

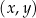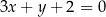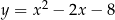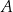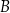W kartezjańskim układzie współrzędnych (x,y) prosta o równaniu 3x + y + 2 = 0 przecina parabolę o równaniu y = x 2 − 2x − 8 w punktach A oraz B , które są kolejnymi wierzchołkami równoległoboku 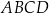ABCD . Wierzchołek 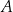A ma pierwszą współrzędną ujemną. Wierzchołek 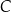C leży na prostej o równaniu 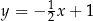y = − 12x + 1 i ma pierwszą współrzędną dodatnią. Odległość punktu 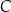C od prostej zawierającej bok 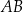AB równoległoboku jest równa 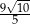-- 9√-10- 5 . Oblicz długość boku 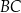BC tego równoległoboku.

Zadanie 12
(6 pkt)

Wyznacz wszystkie wartości parametru 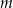m , dla których równanie

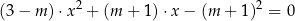
2 2 (3− m) ⋅x + (m + 1)⋅x − (m + 1) = 0

ma dwa różne rozwiązania rzeczywiste 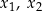x1, x2 spełniające warunek

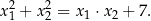
x21 + x22 = x1 ⋅x2 + 7.

Zadanie 13
(6 pkt)

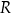Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma wysokości H ostrosłupa oraz promienia R okręgu opisanego na podstawie tego ostrosłupa jest równa 6.

  • Wykaż, że objętość 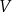V każdego z takich ostrosłupów w zależności od długości 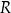R promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem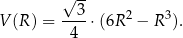

    √ -- 3 V (R ) = ----⋅(6R 2 − R3). 4

  • Wyznacz długość promienia okręgu opisanego na podstawie tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tę największą objętość.

Arkusz Wersja PDF
Rozwiązania