/Szkoła średnia/Zadania maturalne/Matura 2024/Matura próbna

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 13 kwietnia 2024 Czas pracy: 180 minut

Zadanie 1
(2 pkt)

Dane są liczby

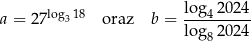
log 18 log42-024- a = 27 3 oraz b = log 2 024 8

Oblicz 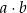a⋅b .

Zadanie 2
(2 pkt)

Prosta postaci 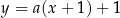y = a(x+ 1)+ 1 jest styczna do wykresu funkcji 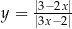|3−2x| y = |3x−2| w punkcie 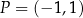P = (− 1,1) . Oblicz a .

Zadanie 3
(3 pkt)

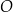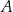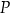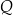Dany jest okrąg O . Przez punkt A poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – P oraz Q . Przez punkt 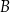B leżący na odcinku 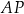AP poprowadzono styczną do tego okręgu w punkcie 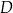D , która przecięła odcinek 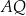AQ w punkcie 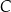C (zobacz rysunek).

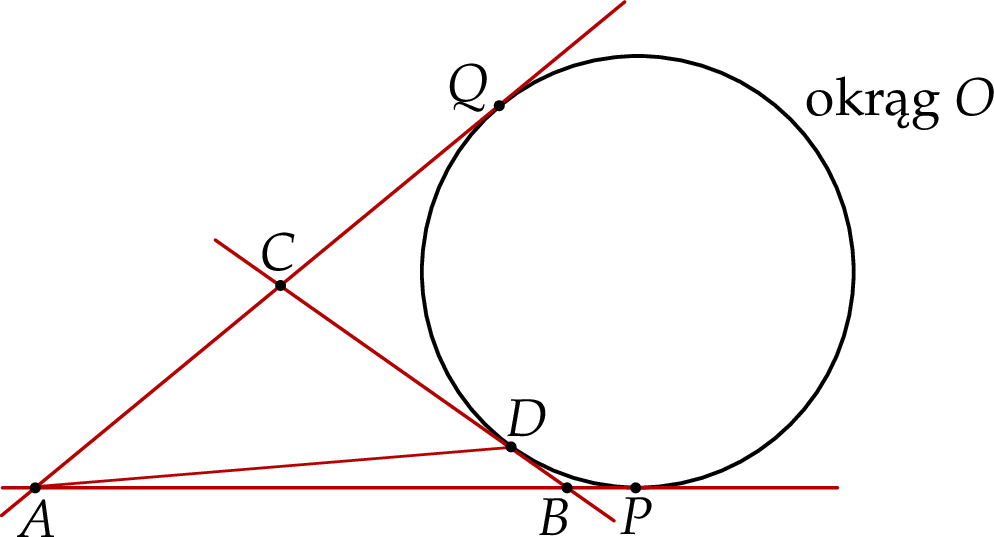
ZINFO-FIGURE

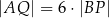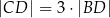Wykaż, że jeżeli |AQ | = 6 ⋅|BP | oraz |CD | = 3 ⋅|BD | , to trójkąt 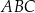ABC nie jest równoramienny.

Zadanie 4
(3 pkt)

Wojtek i Łukasz postanowili rozegrać między sobą dziesięć partii gry w rzutki. Prawdopodobieństwo wygrania pojedynczej partii przez Wojtka jest trzy razy większe, niż prawdopodobieństwo wygrania partii przez Łukasza i każda partia kończy się zwycięstwem jednego z zawodników. Oblicz prawdopodobieństwo tego, że Wojtek nie wygrał wszystkich partii, ale wygrał ich co najmniej 7. Wynik podaj w postaci ułamka zwykłego nieskracalnego.

Zadanie 5
(3 pkt)

Rozwiąż równanie 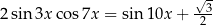√ - 2 sin 3x cos 7x = sin1 0x+ -23 .

Zadanie 6
(3 pkt)

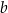Wykaż, że jeżeli liczby dodatnie a i b spełniają warunek

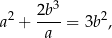
2 2b-3 2 a + a = 3b ,

to spełniają też równość

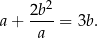
2 a + 2b--= 3b. a

Zadanie 7
(4 pkt)

Wyznacz wszystkie wartości parametru 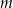m , dla których równanie

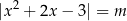
|x2 + 2x − 3| = m

ma cztery różne rozwiązania, których iloczyn jest mniejszy od 5.

Zadanie 8
(4 pkt)

Konstruujemy ciąg trójkątów równobocznych 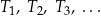T1, T2, T3, ... następująco:

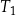  • T1 jest trójkątem równobocznym o polu 1.

  • dla każdego 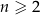n ≥ 2 , trójkąt 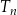Tn ma wierzchołki na trzech różnych bokach trójkąta 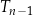Tn−1 i każdy z wierzchołków trójkąta 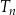Tn dzieli odpowiedni bok trójkąta 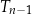Tn −1 w stosunku 1 : 2.

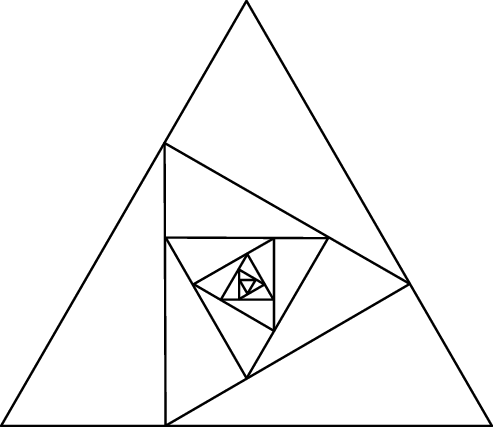
ZINFO-FIGURE

Oblicz sumę pól wszystkich trójkątów 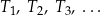T1, T2, T3, ... .

Zadanie 9
(5 pkt)

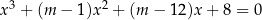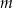Pierwiastki równania x 3 + (m − 1)x2 + (m − 12)x + 8 = 0 z niewiadomą x tworzą trzywyrazowy ciąg geometryczny. Oblicz m oraz sumę kwadratów tych pierwiastków.

Zadanie 10
(5 pkt)

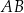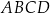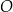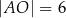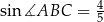Odcinek AB jest dłuższą podstawą trapezu równoramiennego ABCD opisanego na okręgu o środku O . Oblicz pole tego trapezu jeżeli |AO | = 6 i 4 sin ∡ABC = 5 .

Zadanie 11
(5 pkt)

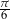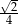Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka tworzą z jego podstawą kąty o miarach π6- i α . Cosinus kąta między tymi przekątnymi jest równy √2- 4 . Wyznacz miarę kąta α .

Zadanie 12
(5 pkt)

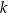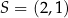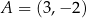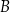Prosta k przecina okrąg o środku S = (2 ,1) w punktach A = (3,− 2) i B , przy czym 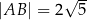√ -- |AB | = 2 5 . Wyznacz równanie prostej k .

Zadanie 13
(6 pkt)

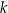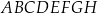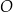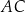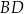Rozważamy wszystkie graniastosłupy prawidłowe czworokątne ABCDEF GH , w których odcinek łączący punkt O przecięcia przekątnych AC i BD podstawy 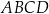ABCD z dowolnym wierzchołkiem podstawy 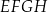EF GH ma długość 3 (zobacz rysunek).

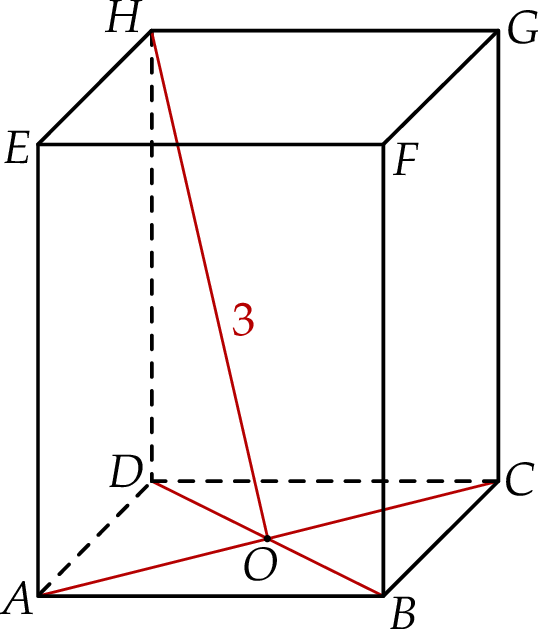
ZINFO-FIGURE

Wyznacz wymiary tego z rozważanych graniastosłupów, którego objętość jest największa. Oblicz tę największą objętość.

Arkusz Wersja PDF
Rozwiązania