/Konkursy/Zadania/Liczby/Wyrażenia algebraiczne/2 literki

Zadanie nr 2376096

Wykaż, że jeżeli liczby dodatnie i 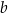spełniają warunek

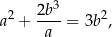
3 a2 + 2b--= 3b2, a

to spełniają też równość

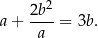
2b-2 a + a = 3b.

Rozwiązanie

Zapiszmy dane wyrażenie tak, żeby nie było mianownika.

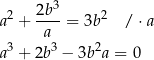
3 a2 + 2b--= 3b2 / ⋅ a a a3 + 2b3 − 3b2a = 0

Sposób I

Zauważmy, że dana równość jest spełniona jeżeli 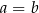a = b , to sugeruje, że w tym wyrażeniu powinno dać się wyłączyć 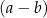(a − b) przed nawias. Próbujemy to zrobić.

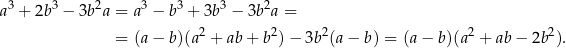
a3 + 2b3 − 3b2a = a3 − b3 + 3b3 − 3b2a = 2 2 2 2 2 = (a − b)(a + ab + b ) − 3b (a − b) = (a − b)(a + ab − 2b ).

Wyrażenie w drugim nawiasie też się zeruje dla 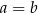a = b , więc nadal próbujemy wyciągnąć 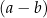(a − b) przed nawias.

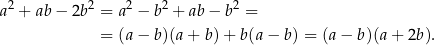
2 2 2 2 2 a + ab − 2b = a − b + ab − b = = (a − b)(a + b) + b(a − b) = (a − b)(a + 2b).

Wiemy zatem, że

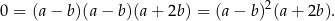
0 = (a − b)(a − b)(a + 2b) = (a − b)2(a + 2b ).

Wiemy dodatkowo, ze i 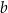są dodatnie, więc 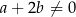a+ 2b ⁄= 0 . W takim razie 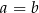a = b . Wtedy faktycznie

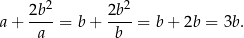
2b-2 2b2- a + a = b+ b = b+ 2b = 3b.

Sposób II

Zauważmy, że dana równość jest jednorodna, tzn. każdy występujący w niej jednomian ma stopień 3. To oznacza, że dość łatwo zamiast dwóch zmiennych możemy zrobić jedną.

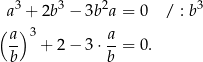
3 3 2 3 a + 2b − 3b a = 0 / : b (a-)3 a- b + 2− 3⋅ b = 0.

Podstawiamy teraz 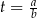t = a b .

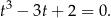
t3 − 3t+ 2 = 0.

Gołym okiem widać, że jednym z pierwiastków tego wielomianu jest 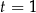t = 1 , więc dzielimy go przez (t − 1) .

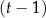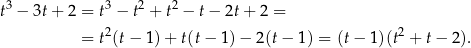
3 3 2 2 t − 3t+ 2 = t − t + t − t− 2t + 2 = = t2(t− 1)+ t(t − 1)− 2(t− 1) = (t− 1 )(t2 + t− 2).

Rozkładamy jeszcze trójmian w drugim nawiasie.

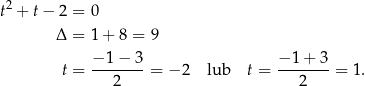
t2 + t − 2 = 0 Δ = 1 + 8 = 9 −-1-−-3 −-1-+-3 t = 2 = − 2 lub t = 2 = 1 .

Mamy zatem

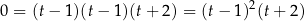
0 = (t − 1)(t− 1)(t+ 2) = (t− 1)2(t + 2)

Zauważmy teraz, że 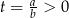t = a > 0 b , więc 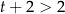t+ 2 > 2 . Zatem 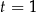t = 1 , czyli 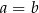a = b . Stąd

2b 2 2b2 a + ----= b+ ----= b+ 2b = 3b. a b

Rozwiązanie Losuj ponownie