/Szkoła średnia/Geometria/Stereometria

Zadanie nr 2789975

Dodaj do ulubionych
Dodaj do rozwiązanych

W ostrosłupie prawidłowym trójkątnym 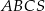ABCS krawędź podstawy ma długość a . Pole powierzchni bocznej tego ostrosłupa jest dwa razy większe od pola jego podstawy. Oblicz cosinus kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.

PIC

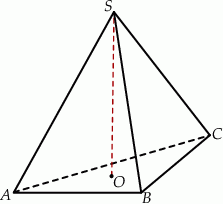
Rozwiązanie

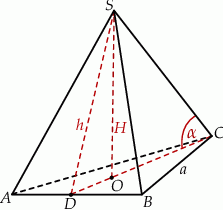
Oznaczmy przez 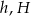h,H odpowiednio długości wysokości ściany bocznej oraz wysokości ostrosłupa.

PIC

Z podanego stosunku pola bocznego do pola podstawy mamy

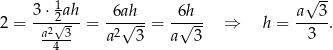
1 √ -- 2 = 3⋅√2ah-= -6a√h--= -6h√--- ⇒ h = a--3. a2-3 a2 3 a 3 3 4

Ponieważ środek 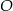O trójkąta równobocznego 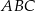ABC dzieli jego wysokość 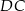DC w stosunku 2:1, mamy

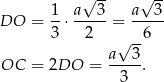
√ -- √ -- DO = 1⋅ a--3-= a--3- 3 2 6 a√ 3- OC = 2DO = ----. 3

Z trójkąta prostokątnego 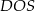DOS obliczamy teraz wysokość ostrosłupa.

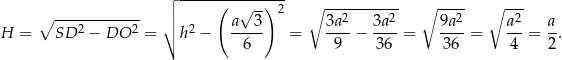
┌│ -----(--√--)-2- ∘ ----------- ∘ ---- ∘ --- ∘ ------------ │∘ a 3 3a2 3a2 9a 2 a2 a H = SD 2 − DO 2 = h2 − ----- = ----− ----= ----= --= --. 6 9 36 36 4 2

Patrzymy teraz na trójkąt prostokątny SOC .

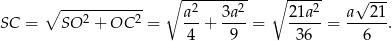
∘ --------- ∘ ----- ∘ ------------ a2 3a2 21a2 a√ 21- SC = SO 2 + OC 2 = ---+ ----= -----= -----. 4 9 36 6

Stąd

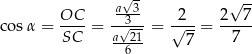
a√-3 √ -- cosα = OC--= -√3--= √2--= 2--7- SC a-21- 7 7 6

 
Odpowiedź: 2√ 7 --7-

Wersja PDF