/Szkoła średnia/Geometria/Stereometria

Zadanie nr 3913184

Dodaj do ulubionych
Dodaj do rozwiązanych

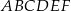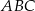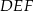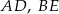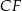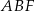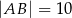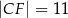Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych AD , BE i CF . Oblicz pole trójkąta ABF wiedząc, że |AB | = 10 i |CF | = 11 . Narysuj ten graniastosłup i zaznacz na nim trójkąt ABF .

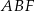Rozwiązanie

Rozpoczynamy od rysunku.

PIC

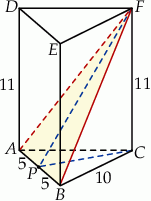
Widać, że trójkąt 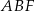ABF jest równoramienny i znamy długość jego podstawy 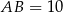AB = 10 . Wystarczy zatem obliczyć długość jego wysokości 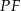PF . Możemy to zrobić korzystając z twierdzenia Pitagorasa w trójkącie 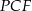P CF . Ze wzoru na długość wysokości w trójkącie równobocznym mamy

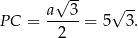
√ -- √ -- P C = a--3-= 5 3. 2

Zatem

∘ ----------- ∘ --√----------- √ --------- P F = P C 2 + CF 2 = (5 3)2 + 112 = 75 + 1 21 = 14.

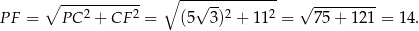
Zatem interesujące nas pole jest równe

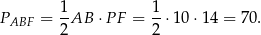
1- 1- PABF = 2 AB ⋅ PF = 2 ⋅10 ⋅14 = 70.

 
Odpowiedź: 70

Wersja PDF