Zadanie nr 4303230
Wśród wszystkich graniastosłupów prawidłowych sześciokątnych, w których suma długości wszystkich krawędzi jest równa 24, jest taki, który ma największe pole powierzchni bocznej. Oblicz długość krawędzi podstawy tego graniastosłupa.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
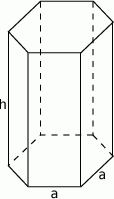
Oznaczmy długość krawędzi podstawy graniastosłupa przez 
, a długość wysokości przez 
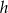. Podana suma długości krawędzi daje równanie
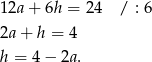
Zatem pole powierzchni bocznej graniastosłupa jest równe
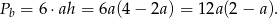
O otrzymanym wyrażeniu należy myśleć jak o funkcji kwadratowej zmiennej 
, przy czym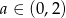 
(bo musi być 
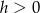). Wykres tej funkcji jest parabolą o ramionach skierowanych w dół, więc największą wartość pola powierzchni bocznej otrzymamy w wierzchołku, czyli dla 
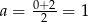(dokładnie w środku między pierwiastkami).
Odpowiedź: 1
