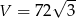Zadanie nr 7642350
Trójkąt 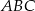 jest podstawą prawidłowego ostrosłupa
jest podstawą prawidłowego ostrosłupa 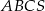 , którego krawędź boczna ma długość 10. Punkt
, którego krawędź boczna ma długość 10. Punkt 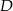 jest środkiem wysokości
jest środkiem wysokości 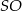 ostrosłupa oraz
ostrosłupa oraz 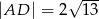 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku
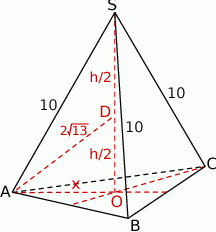
Oznaczmy 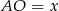 i
i 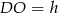 . Z twierdzenia Pitagorasa w trójkątach
. Z twierdzenia Pitagorasa w trójkątach 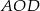 i
i 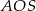 otrzymujemy układ równań
otrzymujemy układ równań
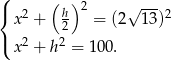
Odejmujemy od drugiego równania pierwsze (żeby skrócić 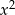 ) i mamy
) i mamy
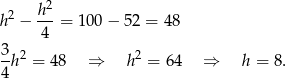
W takim razie z drugiego równania układu mamy
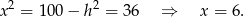
Odcinek 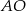 to
to  wysokości trójkąta równobocznego w podstawie ostrosłupa, więc jeżeli oznaczymy
wysokości trójkąta równobocznego w podstawie ostrosłupa, więc jeżeli oznaczymy 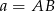 , to
, to
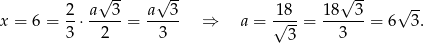
Objętość ostrosłupa jest więc równa
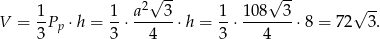
Odpowiedź: