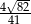Zadanie nr 9292773
Dany jest ostrosłup prawidłowy czworokątny 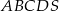 o podstawie
o podstawie 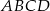 . W trójkącie równoramiennym
. W trójkącie równoramiennym 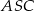 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 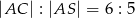 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Rozwiązanie
Rozpoczynamy od rysunku.
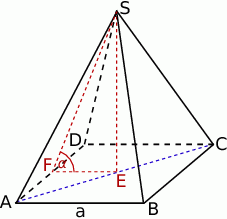
Oznaczmy długość krawędzi podstawy ostrosłupa przez  . Obliczymy w zależności od
. Obliczymy w zależności od  długości odcinków
długości odcinków 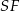 i
i 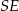 , co pozwoli nam obliczyć sinus kąta
, co pozwoli nam obliczyć sinus kąta  .
.
Z podanego stosunku 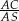 mamy
mamy
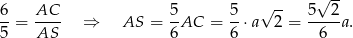
Z trójkąta prostokątnego 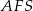 mamy
mamy
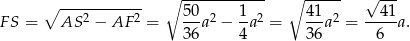
Z trójkąta prostokątnego 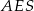 mamy
mamy
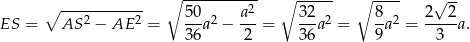
Mamy więc
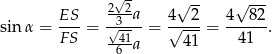
Odpowiedź: