Zadanie nr 9323290
Podstawą ostrosłupa 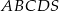 jest prostokąt
jest prostokąt 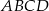 o bokach długości
o bokach długości 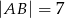 i
i 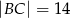 . Krawędź
. Krawędź 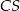 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 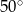 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
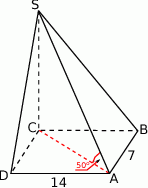
Łatwo obliczyć długość odcinka 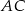 .
.
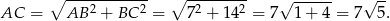
Zatem z trójkąta 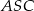 mamy
mamy
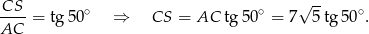
Objętość ostrosłupa jest więc równa
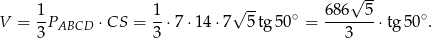
Odpowiedź: