Zadanie nr 9705291
Objętość graniastosłupa prawidłowego trójkątnego jest równa 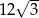 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
, a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
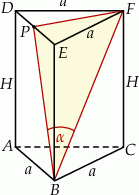
Zanim spróbujemy dokładnie zrozumieć co mamy obliczyć, popatrzmy co mamy dane:
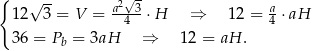
Podstawiając 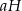 z drugiego równania do pierwszego mamy
z drugiego równania do pierwszego mamy
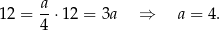
Zatem 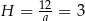 .
.
Teraz popatrzmy czego szukamy. Aby wiedzieć jaki jest kąt między przekątną 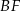 , a ścianą
, a ścianą 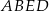 musimy znaleźć rzut tej przekątnej na tę ścianę. Rzut ten będzie odcinkiem, którego jednym końcem będzie
musimy znaleźć rzut tej przekątnej na tę ścianę. Rzut ten będzie odcinkiem, którego jednym końcem będzie 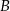 (bo przy rzucie stoi w miejscu), a drugi koniec będzie rzutem punktu
(bo przy rzucie stoi w miejscu), a drugi koniec będzie rzutem punktu 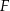 . Zauważmy, że jeżeli
. Zauważmy, że jeżeli 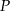 jest środkiem krawędzi
jest środkiem krawędzi 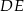 to odcinek
to odcinek 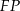 jest prostopadły do płaszczyzny
jest prostopadły do płaszczyzny 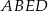 . To oznacza, że rzutem
. To oznacza, że rzutem 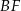 na tę płaszczyznę jest odcinek
na tę płaszczyznę jest odcinek 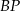 i interesujący nas kąt to
i interesujący nas kąt to 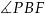 .
.
Trójkąt 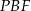 jest prostokątny (bo
jest prostokątny (bo 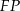 jest prostopadły do płaszczyzny
jest prostopadły do płaszczyzny 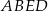 , więc w szczególności do
, więc w szczególności do 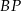 ) zatem
) zatem
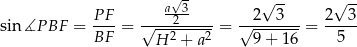
(korzystaliśmy ze wzoru na wysokość w trójkącie równobocznym oraz z twierdzenia Pitagorasa w trójkącie 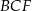 ).
).
Odpowiedź: