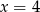Zadanie nr 8565198
Rozwiąż równanie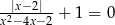 
.
Rozwiązanie
Możemy najpierw sprawdzić czy przypadkiem 2 nie jest pierwiastkiem mianownika (gdyby mianownik dzielił się przez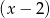 
równanie byłoby dość proste). Okazuje się, że nie, więc przkształcamy normalnie – mnożymy przez mianownik.
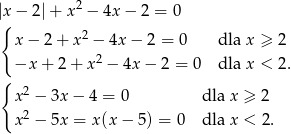
Drugie równanie daje natychmiast rozwiązanie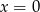 
, pozostaje rozwiązać pierwsze równanie.
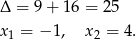
Tylko drugie rozwiązanie spełnia warunek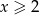 
.
Na koniec musimy sprawdzić, czy przypadkiem któreś z rozwiązań nie zeruje mianownika oryginalnego równania – okazuje się, że tak nie jest.
Odpowiedź: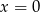 
lub 
