/Szkoła średnia/Zadania maturalne/Matura 2010
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 17 kwietnia 2010 Czas pracy: 180 minut
Podstawą ostrosłupa 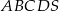 jest prostokąt
jest prostokąt 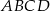 , a krawędź boczna
, a krawędź boczna 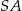 jest jego wysokością. Wykaż, że suma kwadratów pól ścian
jest jego wysokością. Wykaż, że suma kwadratów pól ścian 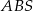 i
i 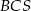 jest równa sumie kwadratów pól ścian
jest równa sumie kwadratów pól ścian 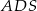 i
i 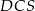 .
.
Rozwiąż równanie 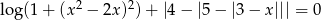 .
.
Wykaż, że jeżeli 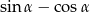 jest liczbą wymierną to wymierna jest również liczba
jest liczbą wymierną to wymierna jest również liczba 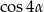 .
.
Przekątne czworokąta 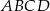 są prostopadłe.
są prostopadłe.
- Wykaż, że sumy kwadratów przeciwległych boków tego czworokąta są równe.
- Wykaż, że jeżeli długości jego boków
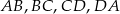 są kolejnymi wyrazami ciągu geometrycznego to czworokąt ten jest rombem.
są kolejnymi wyrazami ciągu geometrycznego to czworokąt ten jest rombem.
Na bokach 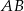 i
i 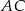 trójkąta
trójkąta 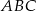 wybrano punkty
wybrano punkty 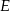 i
i 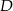 w ten sposób, że
w ten sposób, że 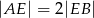 i
i 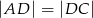 . Punkt
. Punkt 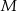 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 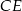 i
i 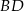 .
.
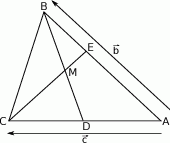
- Przedstaw każdy z wektorów
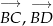 oraz
oraz 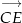 w postaci
w postaci 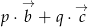 , gdzie
, gdzie 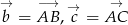 oraz
oraz 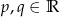 .
. - Korzystając z równości
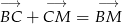 oblicz w jakim stosunku punkt
oblicz w jakim stosunku punkt 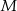 dzieli odcinki
dzieli odcinki 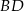 i
i 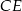 .
.
Wyznacz wszystkie wartości parametrów 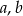 , dla których nierówność
, dla których nierówność
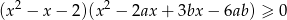
jest spełniona przez każdą liczbę rzeczywistą.
Dany jest czworokąt 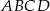 , gdzie
, gdzie 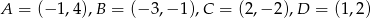 .
.
- Oblicz pole czworokąta
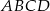 .
. - Oblicz wartość wyrażenia
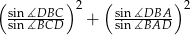 .
.
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej 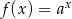 dla
dla 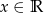 .
.
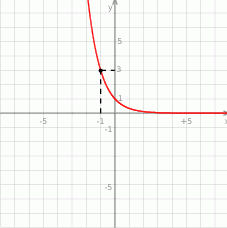
Wykres ten przekształcono w symetrii środkowej względem punktu 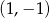 , a następnie w symetrii osiowej względem prostej
, a następnie w symetrii osiowej względem prostej 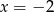 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 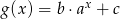 .
.
- Wyznacz liczby
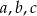 i naszkicuj wykres funkcji
i naszkicuj wykres funkcji 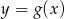 .
. - Odczytaj z wykresu rozwiązanie nierówności
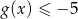 .
.
Odległość środka wysokości stożka od jego powierzchni bocznej jest trzy razy mniejsza niż promień jego podstawy. Oblicz sinus kąta rozwarcia stożka.
Uzasadnij, że liczba 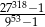 jest liczbą całkowitą.
jest liczbą całkowitą.
Do 12 ponumerowanych szuflad wkładamy losowo 13 pojedynczych skarpetek, przy czym dokładnie dwie z nich tworzą parę. Jakie jest prawdopodobieństwo otrzymania konfiguracji, w której żadna szuflada nie jest pusta oraz skarpetki tworzące parę znajdują się w różnych szufladach.

