/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 6275433

Dodaj do ulubionych
Dodaj do rozwiązanych

W urnie jest dziesięć kul: 4 białe, 3 czarne, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród wylosowanych kul nie ma kul w tym samym kolorze. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.

Rozwiązanie

Za zdarzenia elementarne przyjmujemy trójelementowe zbiory wylosowanych kul, więc

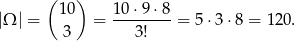
( ) |Ω | = 10 = 10-⋅9-⋅8 = 5⋅3 ⋅8 = 12 0. 3 3!

Zdarzenia sprzyjające obliczymy na dwa sposoby.

Sposób I

Jeżeli wśród wyciągniętych kul nie ma być dwóch kul w tym samym kolorze, to znaczy, że wybraliśmy kule w trzech różnych kolorach. Są cztery możliwości wyboru takich kul:

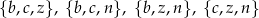
{b,c,z} , {b ,c,n }, {b,z,n}, {c,z,n }

Mamy w tych przypadkach kolejno

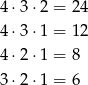
4⋅ 3⋅2 = 24 4⋅ 3⋅1 = 12 4⋅ 2⋅1 = 8 3⋅ 2⋅1 = 6

możliwości wybrania trzech kul. Interesujące nas prawdopodobieństwo jest więc równe

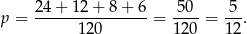
p = 24-+-12-+-8-+-6-= 50--= 5-. 120 120 12

Sposób II

Tym razem obliczmy ile jest zdarzeń, w których są co najmniej 2 kule w tym samym kolorze.

Jeżeli wszystkie trzy kule są tego samego koloru, to albo wszystkie są białe, albo wszystkie są czarne. Jest

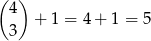
( 4) + 1 = 4 + 1 = 5 3

takich zdarzeń.

Jeżeli są dwie kule zielone, to trzecią kulę możemy wybrać na

4 + 3 + 1 = 8

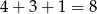
sposobów (wybieramy dowolną z pozostałych).

Jeżeli są 2 czarne kule, to możemy je wybrać na

( ) 3 2 = 3

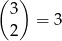
sposoby, a potem dobieramy do nich trzecią kulę na

4 + 2 + 1 = 7

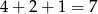
sposobów. Jest więc 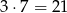3 ⋅7 = 2 1 takich zdarzeń.

Jeżeli wreszcie są 2 białe kule, to możemy je wybrać na

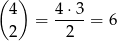
(4 ) 4⋅ 3 = ---- = 6 2 2

sposobów. Do tych kul dobieramy trzecią kule na

3 + 2 + 1 = 6

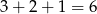
sposobów. Jest więc 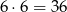6⋅6 = 36 takich zdarzeń i interesujące nas prawdopodobieństwo jest równe

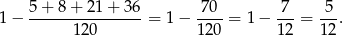
1 − 5+--8+--21+--36-= 1 − -70- = 1 − -7- = -5-. 120 1 20 1 2 1 2

 
Odpowiedź: 152

Wersja PDF