/Szkoła średnia/Prawdopodobieństwo

Zadanie nr 7274912

Dodaj do ulubionych
Dodaj do rozwiązanych

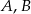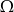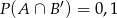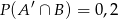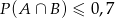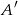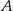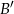Zdarzenia losowe A ,B są zawarte w Ω oraz ′ P(A ∩ B ) = 0,1 i P (A ′ ∩ B) = 0 ,2 . Wykaż, że P (A ∩ B) ≤ 0 ,7 (A ′ oznacza zdarzenie przeciwne do zdarzenia A , B ′ oznacza zdarzenie przeciwne do zdarzenia B ).

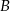Rozwiązanie

Szkicujemy diagram Venna.

PIC

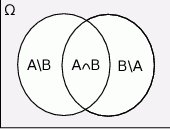
Sposób I

Z obrazka widać, że

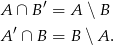
′ A ∩ B = A ∖ B A ′ ∩ B = B ∖A .

W takim razie

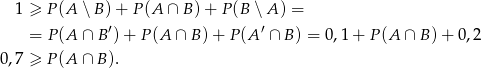
1 ≥ P (A ∖ B) + P (A ∩ B) + P (B ∖A ) = ′ ′ = P (A ∩ B ) + P (A ∩ B )+ P (A ∩ B) = 0 ,1+ P(A ∩ B )+ 0,2 0,7 ≥ P (A ∩ B ).

Sposób II

Oznaczmy 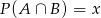P (A ∩ B ) = x . Z obrazka widać, że

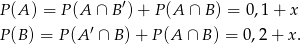
P (A ) = P(A ∩ B′)+ P(A ∩ B ) = 0,1 + x P (B) = P (A ′ ∩ B) + P (A ∩ B ) = 0,2+ x.

Korzystamy teraz ze wzoru na prawdopodobieństwo sumy.

1 ≥ P (A ∪ B ) = P(A ) + P(B )− P(A ∩ B ) 1 ≥ 0,1 + x + 0 ,2+ x − x 0,7 ≥ x .
Wersja PDF