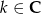Zadanie nr 9131055

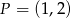Dla jakich wartości parametru odległość punktu P = (1,2) od prostej 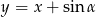y = x+ sin α jest mniejsza lub równa 1√2- .

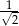Rozwiązanie

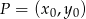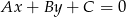Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

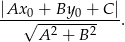
|Ax-0√-+-By-0 +-C|. A 2 + B 2

W naszej sytuacji mamy prostą 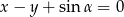x− y+ sin α = 0 , co daje nierówność

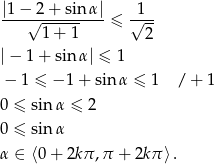
|1-−√2-+-sinα-|≤ √1-- 1+ 1 2 |− 1+ sin α| ≤ 1 − 1 ≤ − 1 + sinα ≤ 1 / + 1 0 ≤ sin α ≤ 2 0 ≤ sin α α ∈ ⟨0 + 2k π,π + 2kπ ⟩.

Odpowiedź: 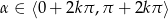α ∈ ⟨0 + 2kπ ,π + 2kπ⟩ , k ∈ C