/Szkoła średnia/Funkcje - wykresy/Homografia

Zadanie nr 1243707

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykres funkcji 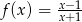x−1- f(x ) = x+1 przekształcono w symetrii względem prostej 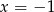x = − 1 i otrzymano wykres funkcji 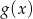g(x) . Wyznacz wzór funkcji g(x) .

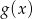Rozwiązanie

Zadanie byłoby proste, gdybyśmy odbijali względem osi 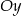Oy . Aby doprowadzić do takiej sytuacji, możemy przesunąć wykres funkcji 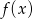f (x) o jedną jednostkę w prawo (tak, aby prosta 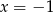x = − 1 przeszła na prostą 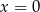x = 0 ), potem odbijemy względem prostej 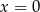x = 0 , a na koniec przesuniemy otrzymany wykres z powrotem, czyli o jedną jednostkę w lewo. O całej operacji można myśleć jak o wyborze innego układu współrzędnych, w którym prosta 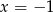x = −1 jest osią Oy .

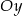Po przesunięciu o 1 jednostkę w prawo otrzymamy funkcję

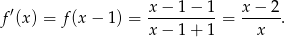
f ′(x ) = f(x − 1) = x−--1−--1-= x-−--2. x− 1+ 1 x

Teraz odbijamy względem osi 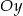Oy

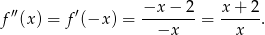
f′′(x ) = f′(−x ) = −x--−-2-= x-+-2. −x x

Na koniec przesuwamy o 1 jednostkę w lewo

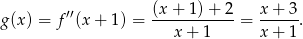
g (x ) = f′′(x + 1 ) = (x-+-1)-+-2-= x+--3. x + 1 x+ 1

Na koniec, dla ciekawskich, wykresy funkcji 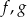f ,g i f′,f′′ .

PIC

 
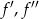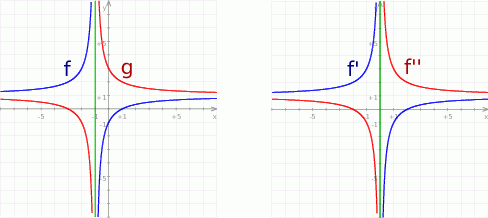
Odpowiedź: g(x ) = xx++31-

Wersja PDF
Rozwiązanie Losuj ponownie