Zadanie nr 2999583
Dla pewnego kąta ostrego  spełniony jest warunek
spełniony jest warunek 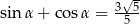 . Oblicz
. Oblicz 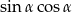 .
.
Rozwiązanie
Liczymy
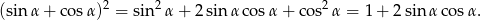
Odejmujemy stronami 1, dzielimy stronami przez 2 i otrzymujemy
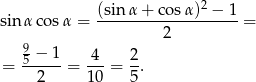
Odpowiedź: 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla pewnego kąta ostrego  spełniony jest warunek
spełniony jest warunek 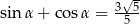 . Oblicz
. Oblicz 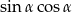 .
.
Liczymy
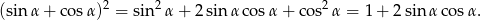
Odejmujemy stronami 1, dzielimy stronami przez 2 i otrzymujemy
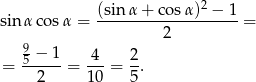
Odpowiedź: 
