Zadanie nr 6659370
Dany jest czworokąt wypukły 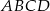 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 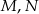 są odpowiednio środkami boków
są odpowiednio środkami boków 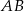 i
i 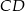 . Punkty
. Punkty 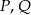 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 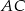 i
i 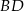 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 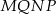 jest równoległobokiem.
jest równoległobokiem.
Rozwiązanie
Rozpoczynamy od rysunku.
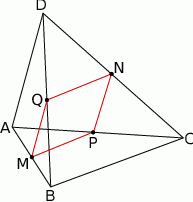
Sposób I
Zauważmy, że odcinek 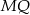 łączy środki boków w trójkącie
łączy środki boków w trójkącie 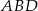 . Jest on więc równoległy do odcinka
. Jest on więc równoległy do odcinka 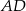 . Podobnie, odcinek
. Podobnie, odcinek 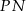 łączy środki boków trójkąta
łączy środki boków trójkąta 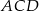 , więc też jest równoległy do
, więc też jest równoległy do 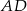 . Zatem
. Zatem

Aby dokończyć dowód wystarczy teraz zauważyć, że odcinki te mają też równą długość
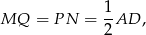
lub wykazać, że odcinki 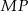 i
i 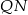 są do siebie równoległe, a tak jest, bo oba są równoległe do
są do siebie równoległe, a tak jest, bo oba są równoległe do 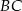 (łączą środki boków w trójkątach
(łączą środki boków w trójkątach 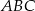 i
i  ).
).
Sposób II
Umieśćmy czworokąt w układzie współrzędnych tak, aby 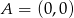 ,
, 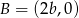 ,
, 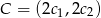 i
i 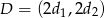 . Wtedy
. Wtedy
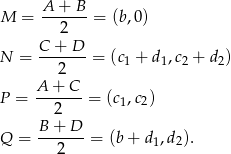
Teraz sprawdzamy, że proste 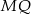 i
i 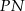 mają takie same współczynniki kierunkowe. Współczynnik kierunkowy prostej
mają takie same współczynniki kierunkowe. Współczynnik kierunkowy prostej 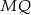 jest równy
jest równy
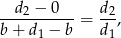
a współczynnik kierunkowy prostej 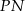 jest równy
jest równy
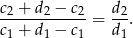
Skoro liczby te są równe, odcinki 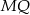 i
i 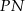 są równoległe.
są równoległe.
Aby dokończyć zadanie, albo zauważamy, że
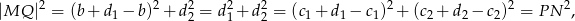
albo sprawdzamy, że proste 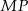 i
i 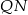 mają takie same współczynniki kierunkowe (tak samo jak powyżej).
mają takie same współczynniki kierunkowe (tak samo jak powyżej).
Sposób III
Zauważmy, że
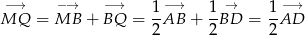
Podobnie,
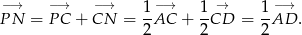
To oznacza, że odcinki 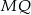 i
i 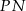 są równoległe i mają równe długości.
są równoległe i mają równe długości.

