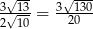Zadanie nr 5627174
Na przyprostokątnych 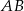 i
i 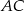 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego 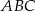 zaznaczono odpowiednio punkty
zaznaczono odpowiednio punkty 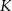 i
i 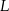 tak, że
tak, że 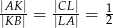 . Odcinki
. Odcinki 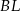 i
i 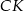 przecinają się w punkcie
przecinają się w punkcie 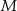 . Oblicz
. Oblicz 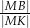 .
.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
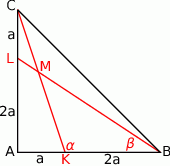
Oznaczmy 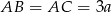 (
(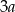 , a nie
, a nie  , żeby nie mieć ułamków) oraz niech
, żeby nie mieć ułamków) oraz niech 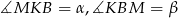 . Stosując twierdzenie sinusów w trójkącie
. Stosując twierdzenie sinusów w trójkącie 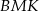 mamy
mamy
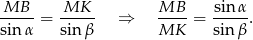
Teraz patrzymy na trójkąt prostokątny 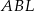 . Mamy w nim
. Mamy w nim
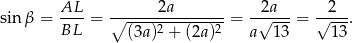
Podobnie wyliczamy 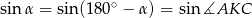 . Patrzymy na trójkąt prostokątny
. Patrzymy na trójkąt prostokątny 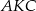 .
.
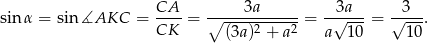
Zatem
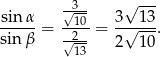
Odpowiedź: