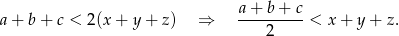Zadanie nr 6316443
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
Rozwiązanie
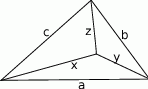
Jeżeli oznaczymy odległości punktu od wierzchołków tak jak na rysunku, to z nierówności trójkąta mamy
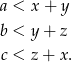
Dodając te nierówności stronami, otrzymujemy