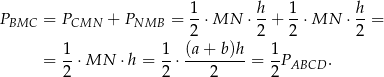/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 4984299

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie 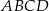ABCD połączono środek 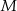M ramienia trapezu 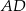AD z końcami drugiego ramienia 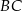BC . Wykaż, że pole powstałego trójkąta 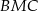BMC jest równe połowie pola trapezu ABCD .

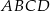Rozwiązanie

Rozpoczynamy od rysunku.

PIC

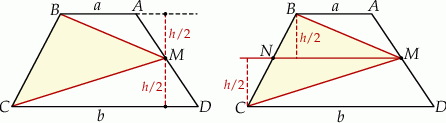
Oznaczmy długości podstaw trapezu przez 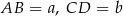AB = a, CD = b , a długość wysokości przez h .

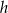Sposób I

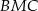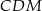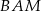Zamiast obliczać pole trójkąta BMC , obliczmy pola trójkątów CDM i BAM . Wysokość w każdym z tych trójkątów jest równa połowie wysokości trapezu. Zatem

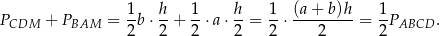
1- h- 1- h- 1- (a-+-b)h- 1- PCDM + PBAM = 2 b⋅ 2 + 2 ⋅a ⋅2 = 2 ⋅ 2 = 2PABCD .

To oznacza, że

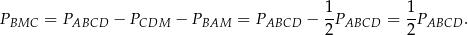
1 1 PBMC = PABCD − PCDM − PBAM = PABCD − --PABCD = -PABCD . 2 2

Sposób II

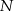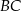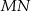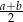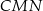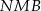Niech N będzie środkiem ramienia BC . Jak wiadomo MN jest równoległy do podstaw trapezu i ma długość a+b -2-- . Ponadto, wysokość w każdym z trójkątów CMN i NMB jest równa 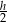h 2 . Zatem

1- h- 1- h- PBMC = PCMN + PNMB = 2 ⋅MN ⋅2 + 2 ⋅MN ⋅ 2 = 1 1 (a + b)h 1 = --⋅MN ⋅h = --⋅---------= -PABCD . 2 2 2 2
Wersja PDF