/Szkoła średnia/Funkcje/Wielomiany/Stopnia 3/Z parametrem

Zadanie nr 9068515

Dany jest wielomian 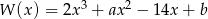3 2 W (x) = 2x + ax − 14x+ b .

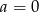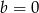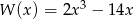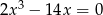  1. Dla a = 0 i b = 0 otrzymamy wielomian W (x) = 2x 3 − 14x . Rozwiąż równanie 2x 3 − 14x = 0 .
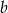  2. Dobierz wartości a i b tak, aby wielomian 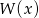W (x) był podzielny jednocześnie przez 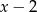x− 2 oraz x+ 3 .
Wersja PDF

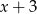Rozwiązanie

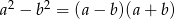  1. Przekształcamy podane równanie (korzystamy ze wzoru: 2 2 a − b = (a− b)(a+ b) ):
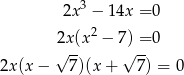
    3 2x − 14x = 0 2x(x2 − 7) = 0 √ -- √ -- 2x(x − 7 )(x+ 7) = 0

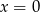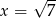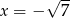    Widać zatem, że lewa strona będzie równa zeru tylko gdy x = 0 , √ -- x = 7 lub √ -- x = − 7 . To są wszystkie rozwiązania tego równania.  
    Odpowiedź: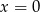 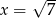x = 0 , √ -- x = 7 lub x = − √ 7-

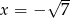
  2. Na mocy twierdzenia Bézout wielomian 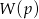W (p ) jest podzielny przez dwumian 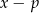x − p wtedy i tylko wtedy gdy 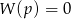W (p) = 0 . Musimy zatem sprawdzić kiedy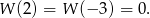
    W (2 ) = W (− 3) = 0.

    Prowadzi to do układu równań:

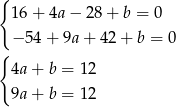
    { 16 + 4a − 28 + b = 0 − 54 + 9a + 42 + b = 0 { 4a + b = 12 9a + b = 12

    Odejmując od drugiego równania pierwsze otrzymamy 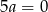5a = 0 , stąd 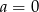a = 0 i b = 12 .  
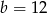    Odpowiedź: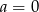 a = 0 ,b = 12

Wersja PDF