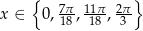/Szkoła średnia/Równania/Trygonometryczne/Stopnia 1

Zadanie nr 4544653

Rozwiąż równanie 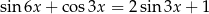sin6x + cos3x = 2sin 3x + 1 w przedziale ⟨0 ,π⟩ .

Wersja PDF

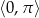Rozwiązanie

Będziemy korzystać ze wzoru

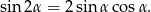
sin 2α = 2 sinα cos α.

Dane równanie możemy zapisać w postaci

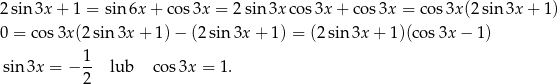
2sin 3x + 1 = sin 6x+ cos3x = 2sin 3x cos3x + co s3x = cos3x (2sin3x + 1) 0 = cos 3x(2 sin 3x + 1) − (2 sin 3x + 1) = (2 sin3x + 1)(cos3x − 1 ) 1 sin 3x = − -- lub cos 3x = 1. 2

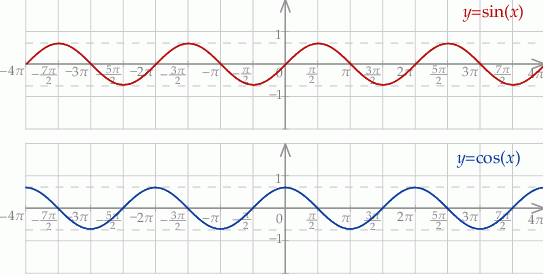
Szkicujemy sinusa i cosinusa i odczytujemy rozwiązanie.

PIC

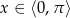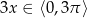Trzeba przy tym trochę uważać, bo wprawdzie x ∈ ⟨0,π⟩ , ale 3x ∈ ⟨0,3π⟩ .

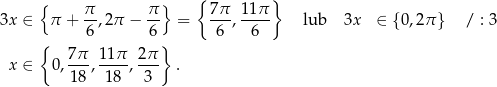
{ } { } 3x ∈ π + π-,2π − π- = 7π-, 11π lub 3x ∈ 0,2π / : 3 6 6 6 6 { } { } x ∈ 0, 7π-, 11-π , 2π . 1 8 18 3

 
Odpowiedź: { 7π- 11π 2π-} x ∈ 0, 18 ,18 , 3

Wersja PDF