Zadanie nr 9792672

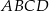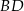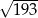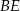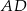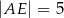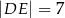W równoległoboku ABCD przekątna ma długość √ ---- 19 3 , a wysokość dzieli bok na odcinki o długościach |AE | = 5 i |DE | = 7 (zobacz rysunek).

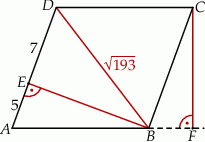
Oblicz długość wysokości 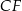tego równoległoboku.

Rozwiązanie

Z twierdzenia Pitagorasa w trójkącie 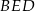BED mamy

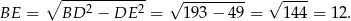
∘ ----2------2 √ --------- √ ---- BE = BD − DE = 193 − 49 = 144 = 12 .

Teraz stosujemy twierdzenie Pitagorasa w trójkącie 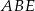ABE

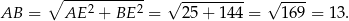
∘ ---2------2 √ --------- √ ---- AB = AE + BE = 25 + 144 = 169 = 13 .

To pozwala obliczyć drugą wysokość równoległoboku – porównujemy dwa wzory na pole.

AD ⋅BE = AB ⋅CF 14 4 12⋅1 2 = 13 ⋅CF ⇒ CF = -13-.

Odpowiedź: 144 1- 13 = 1 113