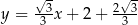Zadanie nr 8114891
Okrąg jest styczny do osi układu współrzędnych w punktach 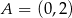 i
i 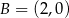 oraz jest styczny do prostej
oraz jest styczny do prostej 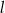 w punkcie
w punkcie 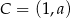 , gdzie
, gdzie 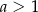 . Wyznacz równanie prostej
. Wyznacz równanie prostej 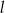 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
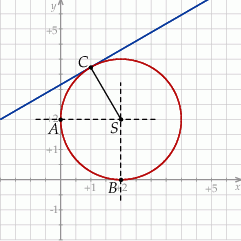
Środek okręgu musi być punktem wspólnym prostych 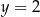 i
i 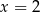 , czyli jest to punkt
, czyli jest to punkt 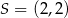 . Promień okręgu jest równy 2, więc okrąg ten ma równanie
. Promień okręgu jest równy 2, więc okrąg ten ma równanie
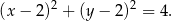
Wiemy, że punkt 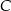 leży na pionowej prostej
leży na pionowej prostej 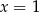 , sprawdźmy jakie punkty okręgu leżą na tej prostej. Podstawiamy
, sprawdźmy jakie punkty okręgu leżą na tej prostej. Podstawiamy 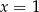 w równaniu okręgu.
w równaniu okręgu.
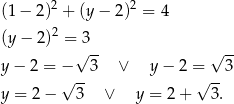
Ponieważ 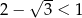 musi być
musi być  .
.
Sposób I
Szukana prosta  to prosta prostopadła do prostej
to prosta prostopadła do prostej  i przechodząca przez punkt
i przechodząca przez punkt 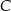 . Można więc napisać równanie prostej
. Można więc napisać równanie prostej 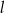 wyznaczając najpierw równanie prostej
wyznaczając najpierw równanie prostej 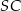 , a potem pisząc równanie prostej prostopadłej przechodzącej przez
, a potem pisząc równanie prostej prostopadłej przechodzącej przez 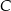 . My jednak skorzystamy z gotowego wzoru na równanie prostej prostopadłej do wektora
. My jednak skorzystamy z gotowego wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/8114891/HzadR17x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 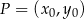
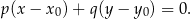
W naszej sytuacji mamy
![→ −→ √ -- √ -- v = SC = [1 − 2,2 + 3 − 2] = [− 1, 3]](https://img.zadania.info/zad/8114891/HzadR20x.gif)
oraz 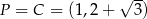 . Prosta
. Prosta 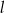 ma więc równanie
ma więc równanie
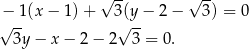
Sposób II
Proste przechodzące przez przez punkt 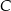 mają postać
mają postać
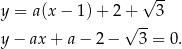
Prosta ta będzie styczna do danego okręgu dokładnie wtedy, gdy jej odległość od punktu 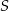 będzie równa 2. Korzystamy ze wzoru na odległość punktu
będzie równa 2. Korzystamy ze wzoru na odległość punktu 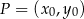 od prostej
od prostej 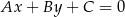 :
:
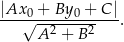
W naszej sytuacji mamy równanie
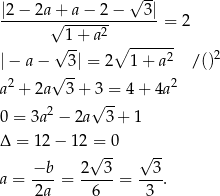
Prosta 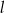 ma więc równanie
ma więc równanie
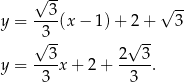
Odpowiedź: 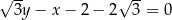 lub równoważnie
lub równoważnie