Zadanie nr 5936453
Punkt 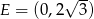 jest środkiem boku
jest środkiem boku 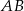 trójkąta równobocznego
trójkąta równobocznego 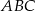 , prosta
, prosta 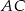 ma równanie
ma równanie 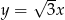 , a początek układu współrzędnych pokrywa się wierzchołkiem
, a początek układu współrzędnych pokrywa się wierzchołkiem 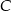 tego trójkąta. Napisz równania wysokości trójkąta
tego trójkąta. Napisz równania wysokości trójkąta 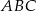 przechodzących przez wierzchołki
przechodzących przez wierzchołki 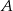 i
i 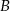 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
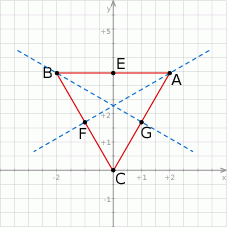
Prosta 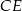 pokrywa się z osią
pokrywa się z osią 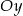 (bo pierwsze współrzędne punktów
(bo pierwsze współrzędne punktów 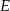 i
i 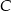 są równe 0) i jest wysokością trójkąta
są równe 0) i jest wysokością trójkąta 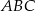 , więc jest prostopadła do boku
, więc jest prostopadła do boku 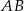 tego trójkąta. W takim razie prosta
tego trójkąta. W takim razie prosta 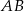 musi być poziomą prostą
musi być poziomą prostą 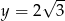 . Obliczamy teraz współrzędne punktu
. Obliczamy teraz współrzędne punktu 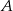 – jest to punkt wspólny prostych
– jest to punkt wspólny prostych 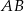 i
i 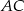 .
.
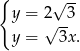
Mamy stąd 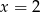 i
i 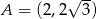 . Wysokość
. Wysokość 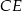 jest osią symetrii trójkąta, więc
jest osią symetrii trójkąta, więc 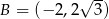 . Środki
. Środki 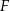 i
i 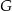 boków
boków 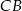 i
i 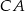 mają współrzędne
mają współrzędne
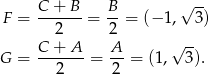
Piszemy teraz równanie wysokości 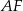 . Szukamy prostej w postaci
. Szukamy prostej w postaci 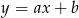 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 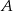 i
i 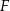 .
.
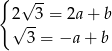
Odejmujemy od pierwszego równania drugie (żeby skrócić 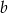 ) i mamy
) i mamy
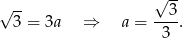
Stąd 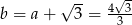 i wysokość
i wysokość 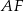 ma równanie
ma równanie 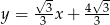 . Analogicznie wyznaczamy równanie prostej
. Analogicznie wyznaczamy równanie prostej 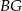 . Szukamy prostej w postaci
. Szukamy prostej w postaci 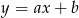 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 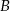 i
i 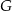 .
.
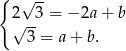
Odejmujemy od pierwszego równania drugie i mamy
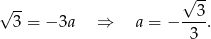
Stąd 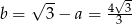 i wysokość
i wysokość 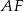 ma równanie
ma równanie 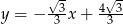 .
.
Odpowiedź: 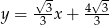 i
i