Zadanie nr 1096964
Punkty 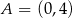 i
i 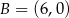 są końcami odcinka
są końcami odcinka 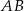 . Prosta
. Prosta 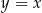 przecina odcinek
przecina odcinek 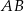 w punkcie
w punkcie 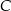 . Oblicz stosunek
. Oblicz stosunek 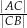 .
.
Rozwiązanie
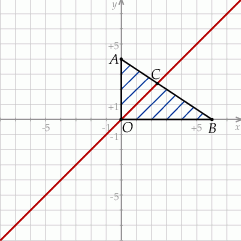
Zaczynamy od rysunku – zauważmy, że dana prosta jest dwusieczną kąta prostego  .
.
Sposób I
Prowadzimy odcinki jak na rysunku (niebieskie odcinki). Na mocy twierdzenia Talesa dorysowane odcinki dzielą odcinek  na 4 równe części, a odcinek
na 4 równe części, a odcinek  na 6 równych części. Zatem stosunek długości odcinków jest równy
na 6 równych części. Zatem stosunek długości odcinków jest równy
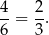
Sposób II
Wyznaczamy równanie prostej 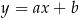 przechodzącej przez punkty
przechodzącej przez punkty 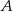 i
i 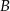
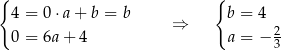
Zatem prosta 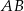 ma równanie
ma równanie 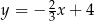 . Obliczamy jej punkt przecięcia z prostą
. Obliczamy jej punkt przecięcia z prostą 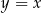 – podstawiamy
– podstawiamy 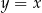 do powyższego równania.
do powyższego równania.
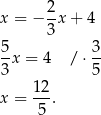
Stad 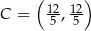 i odcinki
i odcinki 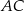 i
i 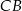 mają długości:
mają długości:
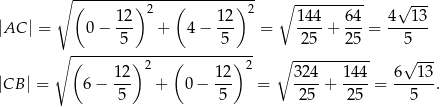
Zatem
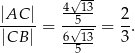
Sposób III
Na mocy twierdzenia o dwusiecznej mamy
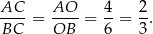
Odpowiedź: