/Konkursy/Zadania/Liczby/Ułamki

Zadanie nr 9900180

Dodaj do ulubionych
Dodaj do rozwiązanych

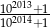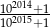Która z liczb jest większa: 102013+-1 102014+ 1 , czy 102014+1 102015+1 ?

Rozwiązanie

Sposób I

Jakoś trzeba zacząć, więc załóżmy np., że pierwsza liczba jest mniejsza od drugiej. Przekształcamy nierówność, żeby się przekonać, czy rzeczywiście tak jest.

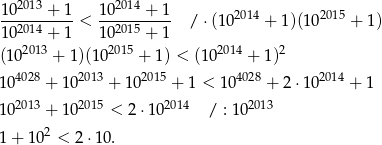
102013 +-1 1-02014-+-1 2014 2015 102014 + 1 < 1 02015 + 1 / ⋅(10 + 1)(1 0 + 1) 2013 2015 2014 2 (10 + 1 )(1 0 + 1) < (1 0 + 1) 104028 + 1 02013 + 102015 + 1 < 104028 + 2⋅10 2014 + 1 102013 + 1 02015 < 2 ⋅102014 / : 102013 2 1+ 10 < 2 ⋅10.

Otrzymana nierówność jest oczywiście nieprawdziwa, więc jednak pierwsza liczba jest większa od drugiej.

Sposób II

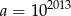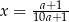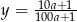Jeżeli oznaczymy 2013 a = 10 to dane liczby możemy zapisać w postaci -a+1- x = 10a+ 1 oraz y = 1100a0a++11 . Obliczymy teraz 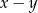x − y i sprawdzimy, czy jest to liczba ujemna, czy dodatnia.

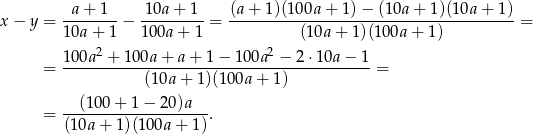
a + 1 10a + 1 (a+ 1)(100a + 1) − (10a + 1)(1 0a+ 1) x − y = --------− ---------= --------------------------------------- = 10a + 1 100a + 1 (1 0a+ 1)(100a + 1) 100a 2 + 1 00a+ a+ 1− 100a2 − 2⋅ 10a− 1 = ------------------------------------------ = (10a + 1 )(1 00a+ 1) --(10-0+-1-−-2-0)a-- = (10a + 1)(1 00a+ 1).

Liczba ta jest ewidentnie dodatnia, czyli 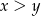x > y .  
Odpowiedź: 102013+1 > 102014+-1 102014+1 102015+ 1

Wersja PDF
Rozwiązanie Losuj ponownie