/Szkoła podstawowa

Zadanie nr 1086999

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ostrosłup prawidłowy czworokątny. Pole powierzchni całkowitej tej bryły jest równe 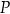P , a jedna ściana boczna ma pole równe 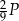29P . Pole powierzchni bocznej tego ostrosłupa jest równe A/B.
A) 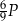6P 9 B) 8P 9
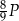
Pole powierzchni podstawy tego ostrosłupa jest dwa razy C/D niż pole powierzchni jego jednej ściany bocznej.
C) mniejsze D) większe

Rozwiązanie

Szkicujemy ostrosłup.

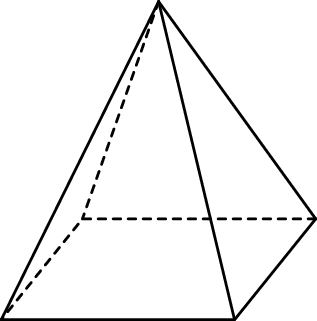
ZINFO-FIGURE

Na pole powierzchni bocznej składają się pola 4 identycznych trójkątów równoramiennych, każdy o polu 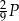29P . Pole powierzchni bocznej jest więc równe

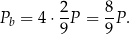
2 8 Pb = 4 ⋅--P = -P. 9 9

Pole podstawy jest więc równe

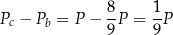
8 1 Pc − Pb = P − -P = -P 9 9

i jest dwa razy mniejsze od pola jednej ściany bocznej.  
Odpowiedź: B, C

Wersja PDF