Zadanie nr 9398491
Ile punktów wspólnych ma prosta 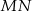 z okręgiem
z okręgiem 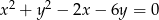 jeśli
jeśli 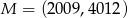 oraz
oraz 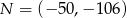 .
.
Rozwiązanie
Rozpocznijmy od napisania równania prostej  . Można to zrobić używając równania prostej przechodzącej przez dwa punkty, ale my obejdziemy się bez tego wzoru: szukamy prostej w postaci
. Można to zrobić używając równania prostej przechodzącej przez dwa punkty, ale my obejdziemy się bez tego wzoru: szukamy prostej w postaci 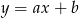 . Podstawiając współrzędne punktów
. Podstawiając współrzędne punktów  i
i  otrzymujemy układ równań
otrzymujemy układ równań

Odejmujemy od pierwszego równania drugie (żeby zredukować 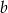 ) i mamy
) i mamy
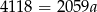
Zatem 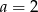 i
i 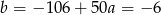 . Równanie prostej
. Równanie prostej 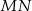 ma więc postać
ma więc postać 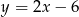 .
.
Sposób I
Podstawiamy 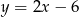 do równania okręgu i sprawdzamy ile rozwiązań ma otrzymane równanie kwadratowe.
do równania okręgu i sprawdzamy ile rozwiązań ma otrzymane równanie kwadratowe.
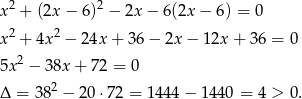
To oznacza, że prosta i okrąg przecinają się w dwóch punktach.
Sposób II
Tym razem przekształćmy równanie okręgu, żeby zobaczyć jaki jest jego środek i promień.
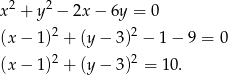
Jest to więc okrąg o środku 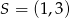 i promieniu
i promieniu 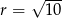 . Aby ustalić jakie jest jego położenie względem prostej
. Aby ustalić jakie jest jego położenie względem prostej  liczymy jak jest odległość punkt
liczymy jak jest odległość punkt 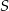 od prostej
od prostej 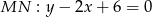 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 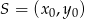 od prostej
od prostej 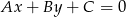 :
:
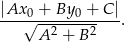
W naszej sytuacji mamy
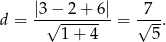
Teraz wystarczy zauważyć, że
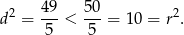
To oznacza, że prosta i okrąg przecinają się w dwóch punktach.
Na koniec obrazek dla ciekawskich.
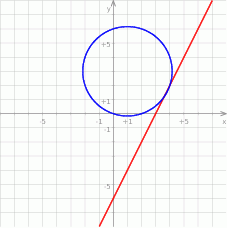
Odpowiedź: 2

