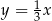/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 4477278

Dodaj do ulubionych
Dodaj do rozwiązanych

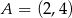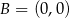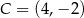Punkty A = (2,4) , B = (0,0 ) , C = (4,− 2) są wierzchołkami trójkąta 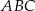ABC . Punkt 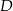D jest środkiem boku 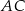AC tego trójkąta. Wyznacz równanie prostej BD .

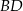Rozwiązanie

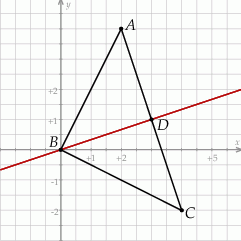
Rozpoczynamy od szkicowego rysunku.

PIC

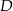Punkt D to środek odcinka 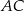AC , więc ma współrzędne

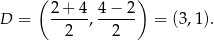
( ) D = 2-+-4-, 4−-2- = (3,1). 2 2

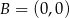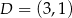Pozostało napisać równanie prostej przechodzącej przez punkty B = (0,0) i D = (3,1 ) . Można skorzystać ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale można też wprost: szukamy prostej postaci 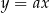y = ax i podstawiamy współrzędne punktu D .

1 1 = 3a ⇒ a = -. 3

 
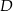Odpowiedź: 1 y = 3x

Wersja PDF