/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 7740199

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz taki punkt 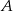A na prostej 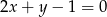2x + y − 1 = 0 , by suma kwadratów jego odległości od osi układu była najmniejsza.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

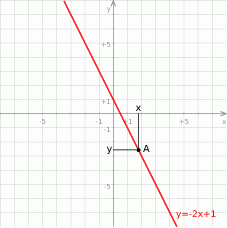
Zauważmy, że jeżeli 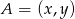A = (x,y) to odległość punktu 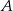A od osi 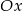Ox jest równa 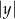|y| , a odległość od osi 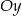Oy wynosi 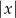|x | . Ponadto, jeżeli 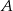A leży na danej prostej to 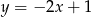y = − 2x+ 1 . Musimy więc wyznaczyć wartość najmniejszą funkcji

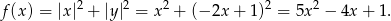
2 2 2 2 2 f (x) = |x| + |y| = x + (− 2x + 1) = 5x − 4x + 1.

Wykres tej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość otrzymamy w wierzchołku, czyli dla

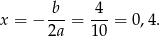
x = − b--= -4- = 0,4. 2a 1 0

Wtedy 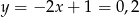y = −2x + 1 = 0,2 .  
Odpowiedź: ( ) A = (0,4;0 ,2 ) = 2 , 1 5 5

Wersja PDF