Zadanie nr 9392032
Punkty 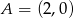 i
i 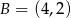 leżą na okręgu o równaniu
leżą na okręgu o równaniu 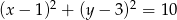 . Wyznacz na tym okręgu taki punkt
. Wyznacz na tym okręgu taki punkt 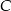 , aby trójkąt
, aby trójkąt 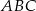 był trójkątem równoramiennym o podstawie
był trójkątem równoramiennym o podstawie 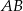 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
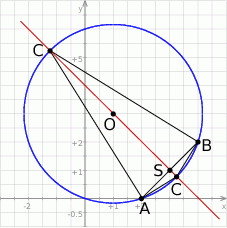
Ponieważ trójkąt 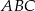 ma być równoramienny, współrzędne punktu
ma być równoramienny, współrzędne punktu 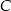 możemy wyznaczyć jako punkt wspólny okręgu i symetralnej odcinka
możemy wyznaczyć jako punkt wspólny okręgu i symetralnej odcinka 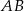 . Symetralną odcinka
. Symetralną odcinka 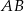 możemy wyznaczyć jak prostą przechodzącą przez
możemy wyznaczyć jak prostą przechodzącą przez 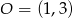 i środek odcinka
i środek odcinka 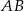
Szukamy prostej 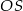 w postaci
w postaci 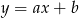 . Podstawiając współrzędne punktów
. Podstawiając współrzędne punktów 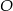 i
i 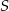 mamy
mamy
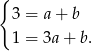
Odejmując od drugiego równania pierwsze mamy 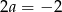 , czyli
, czyli 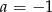 . Stąd
. Stąd 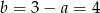 i symetralna odcinka
i symetralna odcinka 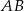 ma równanie
ma równanie 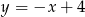 .
.
Szukamy teraz punktów wspólnych tej symetralnej z danym okręgiem – podstawiamy 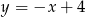 do równania okręgu.
do równania okręgu.
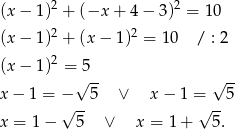
Stąd odpowiednio
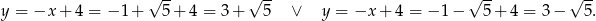
Zatem 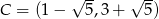 lub
lub 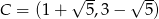 .
.
Odpowiedź: 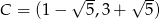 lub
lub