Zadanie nr 3869840
Rozwiąż nierówność 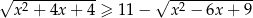 .
.
Rozwiązanie
Łatwo zauważyć, że pod każdym z pierwiastków mamy pełen kwadrat, więc nierówność możemy zapisać w postaci
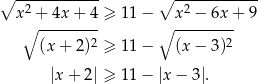
Otrzymaną nierówność rozwiążemy dwoma sposobami.
Sposób I
Aby opuścić wartości bezwzględne rozważamy trzy przypadki.
Jeżeli 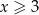 to mamy nierówność
to mamy nierówność
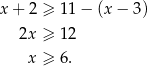
Zatem w tym przypadku rozwiązaniem jest przedział 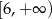 .
.
Jeżeli 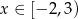 to mamy nierówność
to mamy nierówność
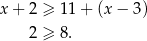
W tym przypadku nierówność jest więc sprzeczna.
Jeżeli wreszcie 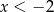 to mamy nierówność
to mamy nierówność
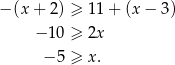
W tym przypadku rozwiązaniem jest więc przedział ![(− ∞ ,− 5]](https://img.zadania.info/zad/3869840/HzadR8x.gif) .
.
Łącząc otrzymane rozwiązania otrzymujemy zbiór rozwiązań:
![(− ∞ ,− 5]∪ [6,+ ∞ ).](https://img.zadania.info/zad/3869840/HzadR9x.gif)
Sposób II
Zapiszmy nierówność w postaci
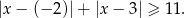
Szukamy zatem liczb (na osi), których suma odległości od 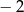 i 3 jest co najmniej równa 11. Naszkicujmy tę sytuację.
i 3 jest co najmniej równa 11. Naszkicujmy tę sytuację.
Zauważmy teraz, że jeżeli ![x ∈ [− 2,3]](https://img.zadania.info/zad/3869840/HzadR13x.gif) to suma odległości od
to suma odległości od 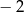 i 3 jest stała i równa 5. Jeżeli natomiast
i 3 jest stała i równa 5. Jeżeli natomiast  jest poza tym przedziałem to suma ta jest tym większa im
jest poza tym przedziałem to suma ta jest tym większa im  jest dalej od końców przedziału. Ponadto łatwo zauważyć, że dla
jest dalej od końców przedziału. Ponadto łatwo zauważyć, że dla 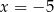 i dla
i dla 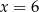 interesująca nas suma jest równa dokładnie 11. Rozwiązaniem nierówności jest więc zbiór
interesująca nas suma jest równa dokładnie 11. Rozwiązaniem nierówności jest więc zbiór
![(− ∞ ,− 5]∪ [6,+ ∞ ).](https://img.zadania.info/zad/3869840/HzadR19x.gif)
Odpowiedź: ![(− ∞ ,− 5]∪ [6,+ ∞ )](https://img.zadania.info/zad/3869840/HzadR20x.gif)

