/Szkoła średnia/Ciągi/Geometryczny/Na dowodzenie

Zadanie nr 3688875

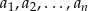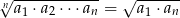Liczby a1,a2,...,an są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość √ ------------ √ ------ na1 ⋅a2⋅⋅⋅an = a1 ⋅ an .

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy przez 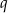q iloraz tego ciągu, to 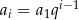i−1 ai = a1q dla i ≥ 1 .

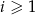Sposób I

Prawa strona danej równości jest równa

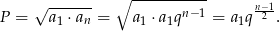
√ ------ ∘ ----------- n−-1 P = a1 ⋅an = a1 ⋅ a1qn−1 = a1q 2 .

Obliczamy teraz lewą stronę (po drodze skorzystamy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego).

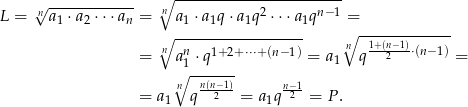
∘ ----------------------- n√ ------------ n 2 n− 1 L = a1 ⋅a2 ⋅⋅⋅an = a1 ⋅ a1q⋅a1q ⋅⋅⋅a1q = ∘ ------------------ n∘ -1+(n−1)------ = n an1 ⋅q1+2+⋅⋅⋅+(n− 1) = a 1 q 2 ⋅(n− 1) = ∘ ------- = a n qn(n−2-1) = a q n−21= P. 1 1

Sposób II

Zauważmy, że dla dowolnego 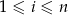1 ≤ i ≤ n mamy

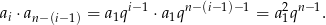
ai ⋅an−(i−1) = a1qi−1 ⋅a1qn−(i−1)−1 = a21qn− 1.

W takim razie

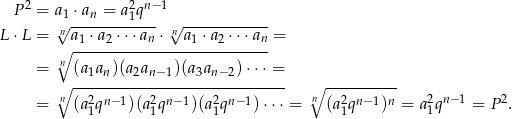
P2 = a 1 ⋅an = a2qn−1 n√ --------1--- √n------------ L ⋅L = ∘ a1 ⋅a2-⋅⋅⋅an-⋅-a1-⋅a2⋅⋅⋅an-= n = (a1an)(a2an− 1)(a3an−2) ⋅⋅⋅ = n∘ ----------------------------- ∘n---------- 2 n− 1 2 = (a21qn− 1)(a 21qn−1)(a21qn− 1)⋅⋅⋅ = (a 21qn−1)n = a1q = P .

Obie strony są dodatnie, więc mamy stąd 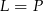L = P .

Wersja PDF