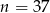Zadanie nr 9644996
W ciągu arytmetycznym 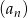 , dla
, dla 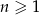 , dane są
, dane są 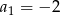 oraz różnica
oraz różnica 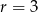 . Oblicz największe
. Oblicz największe  takie, że
takie, że 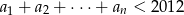 .
.
Rozwiązanie
Korzystamy ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego.
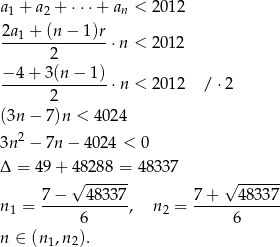
Ponieważ 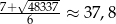 największa możliwa wartość
największa możliwa wartość  to
to 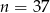 .
.
Odpowiedź: