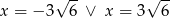/Szkoła średnia/Ciągi/Rekurencyjny/Różne

Zadanie nr 6701016

Wyznacz drugi, trzeci i czwarty wyraz ciągu określonego wzorem rekurencyjnym:

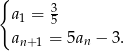
{ a1 = 35 a = 5an − 3. n+ 1

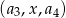Dla wyznaczonych wyrazów znajdź taką liczbę , aby ciąg (a3,x,a4) był ciągiem geometrycznym.

Rozwiązanie

Liczymy

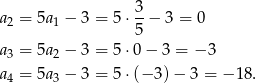
3 a2 = 5a1 − 3 = 5 ⋅--− 3 = 0 5 a3 = 5a2 − 3 = 5 ⋅0− 3 = − 3 a = 5a3 − 3 = 5 ⋅(− 3)− 3 = − 18. 4

Pozostało sprawdzić, kiedy ciąg 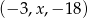(− 3,x,− 18) jest ciągiem geometrycznym. Tak będzie, gdy kwadrat środkowego wyrazu będzie iloczynem wyrazów sąsiednich.

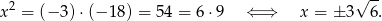
√ -- x2 = (− 3) ⋅(− 18) = 54 = 6⋅9 ⇐ ⇒ x = ± 3 6 .

Odpowiedź: √ -- √ -- x = − 3 6 ∨ x = 3 6

Wersja PDF