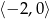Zadanie nr 7012075

Rozwiąż nierówność 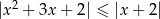2 |x + 3x + 2| ≤ |x + 2| .

Rozwiązanie

Rozłóżmy najpierw trójmian, który jest z lewej strony nierówności.

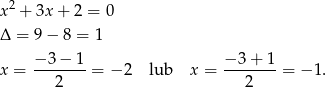
2 x + 3x+ 2 = 0 Δ = 9 − 8 = 1 − 3 − 1 − 3 + 1 x = ------- = − 2 lub x = ------- = − 1. 2 2

Daną nierówność możemy więc zapisać w postaci

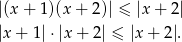
|(x + 1)(x + 2)| ≤ |x + 2| |x + 1|⋅|x + 2| ≤ |x + 2|.

Oczywiście 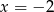x = −2 spełnia tę nierówność. Jeżeli natomiast 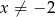x ⁄= − 2 , to możemy ją podzielić stronami przez |x + 2 | .

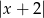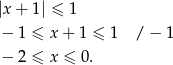
|x+ 1| ≤ 1 − 1 ≤ x + 1 ≤ 1 / − 1 − 2 ≤ x ≤ 0.

Rozwiązaniem nierówności jest więc przedział

⟨− 2,0⟩.

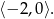
Odpowiedź: ⟨− 2,0⟩