Zadanie nr 2278237
Zbiór 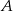 jest zbiorem liczb rzeczywistych, których odległość na osi liczbowej od (-3) jest większa niż 2. Zbiór
jest zbiorem liczb rzeczywistych, których odległość na osi liczbowej od (-3) jest większa niż 2. Zbiór 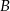 jest przedstawiony na osi liczbowej.
jest przedstawiony na osi liczbowej.
![]()
- Opisz zbiory
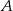 i
i 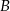 za pomocą nierówności z wartością bezwzględną.
za pomocą nierówności z wartością bezwzględną. - Podaj przykład liczby niewymiernej, która należy jednocześnie do zbioru
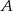 i do zbioru
i do zbioru 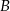 .
.
Rozwiązanie
- Korzystamy z faktu, że liczba
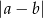 jest równa odległości między punktami osi
jest równa odległości między punktami osi  i
i 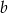 . Zbiór
. Zbiór 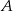 jest więc opisany nierównością
jest więc opisany nierównością 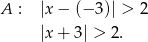
Z obrazka widać, że zbiór
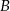 jest zbiorem punktów odległych od -1 o nie więcej niż 1. Zatem
jest zbiorem punktów odległych od -1 o nie więcej niż 1. Zatem 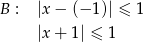
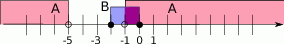
- Liczba ta musi być w przedziale
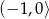 . Taką liczbą jest np.
. Taką liczbą jest np. 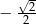 .
.

