Zadanie nr 9392882
Punkty 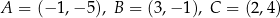 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 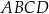 . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
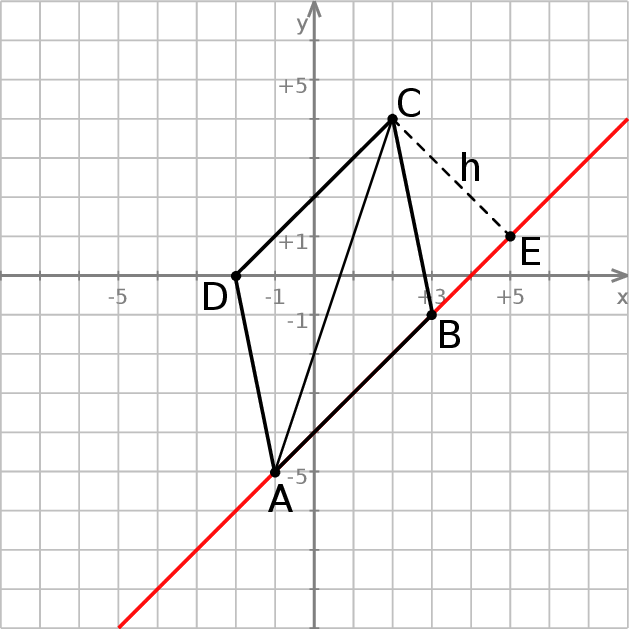
Sposób I
Zauważmy, że równoległobok 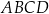 składa się z dwóch przystających trójkątów
składa się z dwóch przystających trójkątów 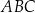 i
i 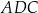 . Wystarczy zatem obliczyć pole trójkąta
. Wystarczy zatem obliczyć pole trójkąta 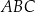 , a to możemy łatwo zrobić ze wzoru
, a to możemy łatwo zrobić ze wzoru
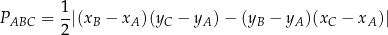
na pole trójkąta o wierzchołkach 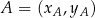 ,
, 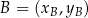 i
i 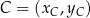 . Liczymy
. Liczymy
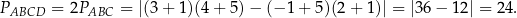
Sposób II
Obliczmy najpierw długość podstawy 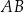
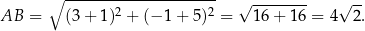
Wyznaczmy jeszcze równanie prostej 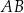 – szukamy prostej w postaci
– szukamy prostej w postaci 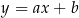 . Podstawiamy współrzędne punktów
. Podstawiamy współrzędne punktów 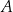 i
i 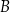 i mamy
i mamy
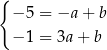
Odejmując od drugiego równania pierwsze (żeby skrócić 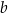 ), mamy
), mamy 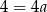 , czyli
, czyli 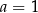 i
i 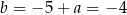 . Prosta
. Prosta 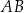 ma więc równanie
ma więc równanie 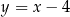 .
.
Wysokość równoległoboku możemy obliczyć ze wzoru na odległość punktu 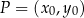 od prostej
od prostej 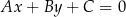 :
:
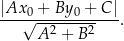
W naszej sytuacji mamy 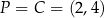 , a prosta to
, a prosta to 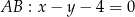 . Mamy zatem
. Mamy zatem
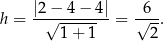
Pole równoległoboku jest więc równe
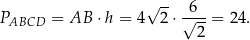
Sposób III
Jeżeli ktoś nie chce korzystać ze wzoru na odległość punktu od prostej, to wysokość równoległoboku możemy wyznaczyć bardziej wprost, wyznaczając równanie wysokości opuszczonej z wierzchołka 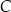 na bok
na bok 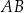 .
.
Rozpoczynamy tak jak w poprzednim sposobie od wyliczenia
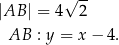
Prosta zawierająca wysokość opuszczoną z wierzchołka 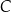 jest prostopadła do
jest prostopadła do 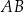 , jest to więc prosta postaci
, jest to więc prosta postaci 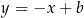 . Współczynnik
. Współczynnik 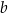 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 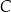 .
.

Zatem wysokość ta ma równanie 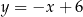 . Wyznaczamy teraz punkt
. Wyznaczamy teraz punkt 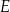 wspólny tej wysokości i podstawy
wspólny tej wysokości i podstawy 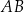
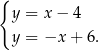
Dodając równania układu stronami mamy 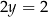 , czyli
, czyli 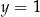 i
i 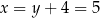 . Zatem
. Zatem 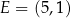 i wysokość równoległoboku jest równa
i wysokość równoległoboku jest równa
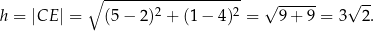
Pole równoległoboku jest więc równe
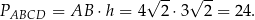
Odpowiedź: 24

