Zadanie nr 2325360

Punkt 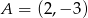A = (2,− 3) jest wierzchołkiem rombu 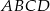ABCD o polu równym 300. Punkt 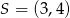S = (3 ,4 ) jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku

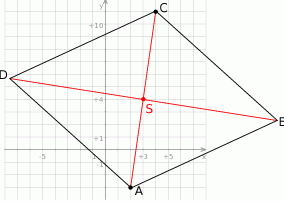
Widać, że mając podane współrzędne punktów 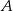i 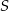łatwo jest wyliczyć współrzędne punktu 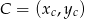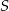C = (xc,yc) . jest środkiem odcinka 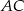, więc

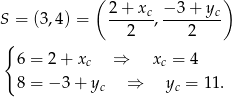
( ) 2-+-xc-−-3-+-yc S = (3,4) = 2 , 2 { 6 = 2+ xc ⇒ xc = 4 8 = − 3+ y ⇒ y = 11. c c

Zatem 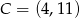C = (4,11) . Ponadto

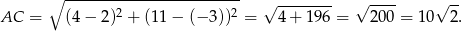
∘ ------------------------ √ -------- √ ---- √ -- AC = (4 − 2)2 + (11 − (− 3))2 = 4 + 19 6 = 200 = 10 2.

Obliczyliśmy długość przekątnej 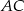, bo ze wzoru na pole rombu z przekątnymi możemy teraz wyliczyć długość drugiej przekątnej

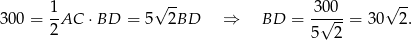
√ -- √ -- 300 = 1AC ⋅BD = 5 2BD ⇒ BD = -3√00--= 30 2 . 2 5 2

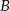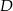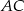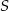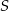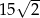Musimy więc znaleźć punkty i , które leżą na prostej prostopadłej do i przechodzącej , i które są odległe od o 15√ 2- . Można to zrobić na różne sposoby.

Sposób I

Jeżeli oznaczymy przez − → SD = [p ,q] to wiemy, że

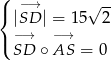
( { −→ √ -- |−SD→ | =−→15 2 ( SD ∘ AS = 0

(pierwszy warunek mówi o długości wektora 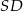, a drugi o jego prostopadłości do przekątnej 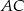). Ponieważ −A→S = [1,7] , powyższe warunki możemy zapisać w postaci

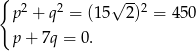
{ 2 2 √ --2 p + q = (1 5 2) = 450 p + 7q = 0.

Podstawiając 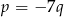p = − 7q z drugiego równania do pierwszego mamy

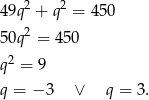
49q2 + q2 = 450 50q2 = 45 0 2 q = 9 q = − 3 ∨ q = 3 .

Zatem −→ SD = [21,− 3] lub −→ SD = [− 21,3] . Daje to odpowiednio

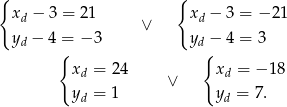
{ { xd − 3 = 21 ∨ xd − 3 = −2 1 yd − 4 = − 3 yd − 4 = 3 { { xd = 24 xd = − 18 y = 1 ∨ y = 7. d d

Zatem pozostałe wierzchołki rombu mają współrzędne 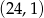(24,1) i (− 18,7) .

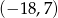Sposób II

Jeżeli nie chcemy korzystać z własności iloczynu skalarnego, to możemy wprost napisać równanie prostej 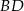i znaleźć na niej punkty leżące w odpowiedniej odległości od .

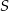Równanie prostej 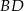można napisać pisząc najpierw równanie prostej 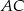, a potem prostej prostopadłej przechodzącej do niej przechodzącej przez 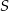. My jednak odrobinę skrócimy sobie drogę i skorzystamy ze wzoru na równanie prostej przechodzącej przez punkt 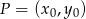P = (x ,y ) 0 0 i prostopadłej do wektora → v = [p,q]

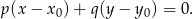
p(x − x0) + q(y − y0) = 0 .

W naszej sytuacji 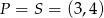P = S = (3,4) i −→ →v = AS = [1,7] . Zatem prosta 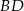ma równanie

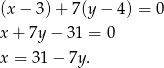
(x− 3)+ 7(y− 4) = 0 x+ 7y − 31 = 0 x = 31 − 7y .

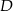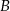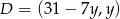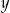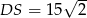Zatem punkt (i też ) ma współrzędne postaci D = (31 − 7y ,y) . Pozostało teraz sprawdzić dla jakiego mamy √ -- DS = 15 2 . Liczymy (od razu porównujemy kwadraty odległości)

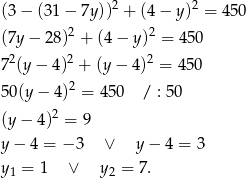
2 2 (3 − (31 − 7y)) + (4 − y) = 4 50 (7y − 28 )2 + (4 − y)2 = 4 50 72(y − 4)2 + (y − 4)2 = 45 0 2 50(y − 4 ) = 450 / : 50 (y − 4)2 = 9 y − 4 = − 3 ∨ y− 4 = 3 y1 = 1 ∨ y2 = 7.

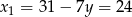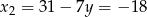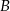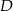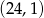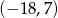Mamy wtedy x = 31 − 7y = 24 1 i x = 31− 7y = − 18 2 odpowiednio. To oznacza, że punkty i mają współrzędne (24 ,1 ) i (− 1 8,7) odpowiednio.
Odpowiedź: 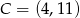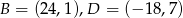C = (4,11) , B = (24,1),D = (− 1 8,7) lub D = (24,1 ),B = (− 18,7)