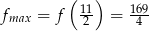/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem

Zadanie nr 8091268

Dodaj do ulubionych
Dodaj do rozwiązanych

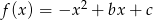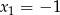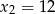Funkcja kwadratowa 2 f(x ) = −x + bx + c ma dwa miejsca zerowe: x1 = − 1 i x2 = 12 . Oblicz największą wartość tej funkcji.

Rozwiązanie

Sposób I

Na mocy wzorów Viète’a mamy

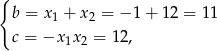
{ b = x1 + x2 = − 1 + 12 = 11 c = −x 1x2 = 12 ,

czyli

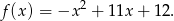
f(x ) = −x 2 + 11x + 12.

Ponadto, pierwsza współrzędna wierzchołka paraboli będącej wykresem funkcji 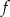f jest równa

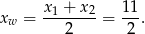
x1-+-x2- 11- xw = 2 = 2 .

Największa wartość funkcji jest więc równa

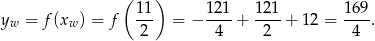
( ) y = f(x ) = f 11- = − 1-21 + 121-+ 12 = 16-9. w w 2 4 2 4

Sposób II

Podstawiamy podane wartości funkcji do danego wzoru funkcji 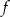f i otrzymujemy układ równań

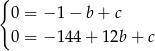
{ 0 = − 1 − b + c 0 = − 14 4+ 1 2b+ c

Odejmujemy od drugiego równania pierwsze (żeby skrócić c ) i mamy

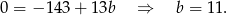
0 = − 143+ 13b ⇒ b = 11.

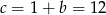Stąd c = 1 + b = 12 i

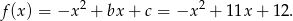
f(x) = −x 2 + bx+ c = −x 2 + 11x + 12.

Pierwsza współrzędna wierzchołka paraboli będącej wykresem tej funkcji jest równa

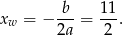
-b- 11- xw = − 2a = 2 .

Największa wartość funkcji jest więc równa

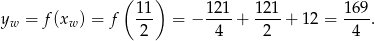
( ) y = f(x ) = f 11- = − 1-21 + 121-+ 12 = 16-9. w w 2 4 2 4

Sposób III

Wiemy jakie są pierwiastki funkcji kwadratowej oraz znamy współczynnik przy 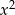x 2 , więc funkcja 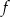f musi mieć wzór

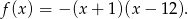
f(x ) = − (x+ 1)(x − 12).

Ponadto, pierwsza współrzędna wierzchołka paraboli będącej wykresem funkcji 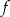f jest równa

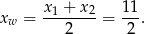
x1 + x2 11 xw = ---2----= 2-.

Największa wartość funkcji jest więc równa

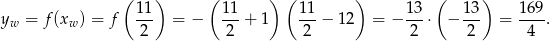
( ) ( ) ( ) ( ) 11- 11- 11- 13- 13- 169- yw = f(xw) = f 2 = − 2 + 1 2 − 12 = − 2 ⋅ − 2 = 4 .

 
Odpowiedź: ( 11) 169 fmax = f 2 = 4

Wersja PDF