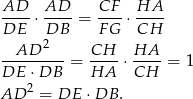Zadanie nr 5775293
Odcinki 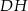 i
i 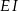 są równoległe do boku
są równoległe do boku 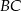 trójkąta
trójkąta 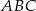 , a odcinki
, a odcinki 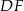 i
i 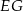 są równoległe do boku
są równoległe do boku 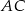 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 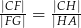 , to
, to 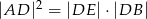 .
.
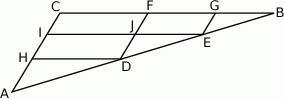
Rozwiązanie
Na danym obrazku mamy wiele podobnych trójkątów i cała trudność polega na wykorzystaniu właściwych z nich. Ponieważ interesują nas długości odcinków 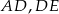 i
i 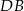 patrzymy na trójkąty
patrzymy na trójkąty 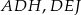 i
i 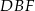 . Z podobieństwa trójkątów
. Z podobieństwa trójkątów 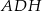 i
i 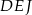 mamy
mamy
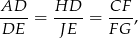
a z podobieństwa trójkątów 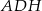 i
i 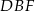 mamy
mamy
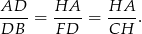
Mnożymy teraz te dwie równości stronami i korzystamy z warunku 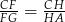 .
.