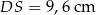/Szkoła podstawowa/Geometria/Czworokąty/Prostokąt

Zadanie nr 9311761

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest prostokąt 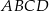ABCD o wymiarach 12 cm i 16 cm. Odcinek 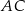AC jest przekątną tego prostokąta. Odcinek 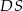DS jest wysokością trójkąta 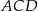ACD (patrz rysunek).

PIC

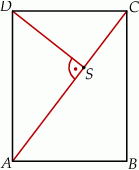
Oblicz długość odcinka 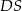DS .

Rozwiązanie

Na mocy twierdzenia Pitagorasa przekątna 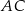AC ma długość

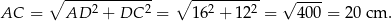
∘ ----2------2 ∘ ---2-----2 √ ---- AC = AD + DC = 1 6 + 1 2 = 400 = 2 0 cm .

Pole trójkąta 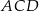ACD to połowa pola prostokąta, czyli jest równe

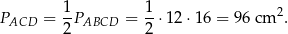
1 1 PACD = -PABCD = --⋅12 ⋅16 = 9 6 cm 2. 2 2

Zauważmy teraz, że interesujący nas odcinek 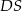DS jest wysokością tego trójkąta opuszczoną na bok 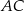AC , więc

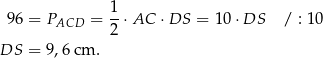
1 96 = PACD = --⋅AC ⋅DS = 10 ⋅DS / : 10 2 DS = 9,6 cm .

 
Odpowiedź: DS = 9,6 cm

Wersja PDF