Zadanie nr 7421993
Uzasadnij, że liczba 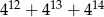 jest podzielna przez 42.
jest podzielna przez 42.
Rozwiązanie
Zauważmy, że
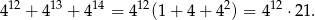
Widać teraz, że liczba ta dzieli się przez 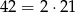 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że liczba 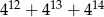 jest podzielna przez 42.
jest podzielna przez 42.
Zauważmy, że
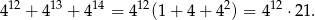
Widać teraz, że liczba ta dzieli się przez 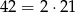 .
.
