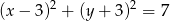Zadanie nr 9781805
Wyznacz równanie okręgu, który jest symetryczny do okręgu o równaniu
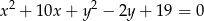
względem prostej 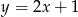 .
.
Rozwiązanie
Przekształćmy dane równanie okręgu tak, aby było widać jaki ma środek i promień.
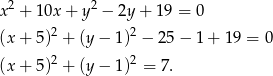
Teraz możemy wykonać szkicowy rysunek.
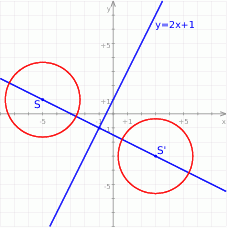
Widać, że okrąg symetryczny do danego okręgu będzie miał taki sam promień – musimy tylko wyznaczyć jego środek 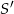 . Rozpocznijmy od napisania równania prostej prostopadłej do danej prostej
. Rozpocznijmy od napisania równania prostej prostopadłej do danej prostej 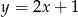 i przechodzącej przez punkt
i przechodzącej przez punkt 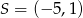 . Prosta ta ma postać
. Prosta ta ma postać 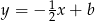 . Współczynnik
. Współczynnik 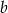 obliczymy podstawiając współrzędne punktu
obliczymy podstawiając współrzędne punktu 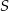 .
.
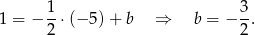
Zatem prosta 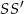 ma równanie
ma równanie 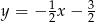 .
.
Sposób I
Wyznaczmy punkt wspólny 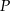 prostych
prostych 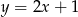 i
i 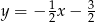 .
.
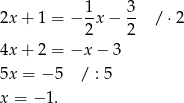
Stąd 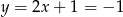 i
i 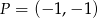 . Współrzędne punktu
. Współrzędne punktu 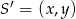 możemy teraz wyliczyć z zależności
możemy teraz wyliczyć z zależności 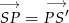 .
.
![−→ −→ SP = PS ′ [−1 + 5 ,− 1 − 1] = [x + 1,y + 1] [4,− 2] = [x + 1 ,y + 1 ].](https://img.zadania.info/zad/9781805/HzadR19x.gif)
Stąd 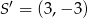 i szukane równanie okręgu ma postać
i szukane równanie okręgu ma postać
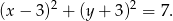
Sposób II
Tak jak w poprzednim sposobie wyznaczamy współrzędne punktu 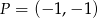 przecięcia prostych
przecięcia prostych 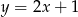 i
i 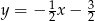 . Teraz wyznaczamy współrzędne punktu
. Teraz wyznaczamy współrzędne punktu 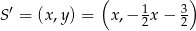 z warunku
z warunku
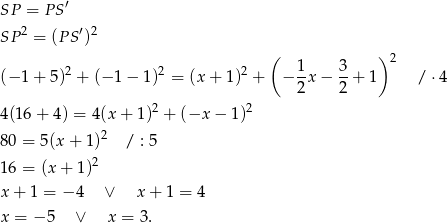
Pierwsze rozwiązanie daje współrzędne punktu 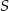 , zatem
, zatem 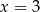 i
i 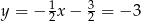 . Wtedy
. Wtedy 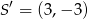 i szukane równanie okręgu ma postać
i szukane równanie okręgu ma postać
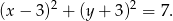
Sposób III
Zauważmy, że długość odcinka 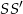 jest dwa razy większa niż odległość punktu
jest dwa razy większa niż odległość punktu 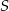 od osi symetrii. Zatem
od osi symetrii. Zatem
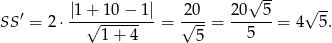
Szukamy teraz na prostej 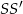 punktu, którego odległość od
punktu, którego odległość od 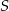 jest równa
jest równa 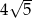 . Szukamy punktu
. Szukamy punktu 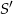 w postaci
w postaci 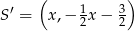 .
.
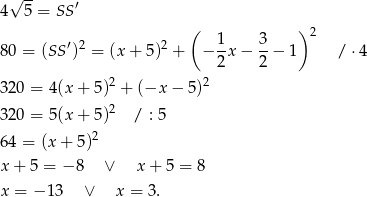
Nawet ze szkicowego rysunku widać, że 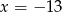 daje punkt leżący po tej samej stronie osi symetrii, co punkt
daje punkt leżący po tej samej stronie osi symetrii, co punkt 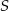 . Zatem
. Zatem 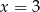 i
i 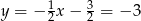 . Stąd
. Stąd 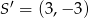 i szukane równanie okręgu ma postać
i szukane równanie okręgu ma postać
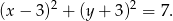
Odpowiedź: