Zadanie nr 9141445
Podstawą ostrosłupa prawidłowego trójkątnego 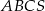 jest trójkąt
jest trójkąt 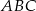 . Kąt nachylenia krawędzi bocznej
. Kąt nachylenia krawędzi bocznej 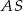 do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi
do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi 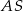 i
i 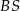 zawartymi w ścianie bocznej
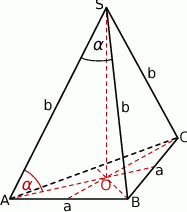
zawartymi w ścianie bocznej 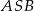 tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
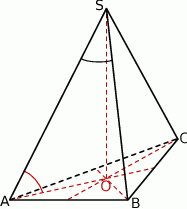
Rozwiązanie
Oznaczmy szukany kąt przez  , długość krawędzi podstawy prze
, długość krawędzi podstawy prze  , a długość krawędzi bocznej przez
, a długość krawędzi bocznej przez 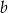 .
.
Dość łatwo jest zauważyć, że możemy napisać dwa równania wiążące ze sobą 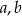 i
i  – jedno równanie to twierdzenie cosinusów w trójkącie
– jedno równanie to twierdzenie cosinusów w trójkącie 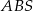 , a drugie to definicja cosinusa w trójkącie
, a drugie to definicja cosinusa w trójkącie 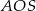 .
.
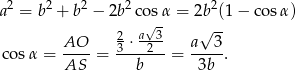
Dalsze rozwiązanie przeprowadzimy dwoma sposobami.
Sposób I
Wyliczamy z drugiego równania
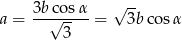
i podstawiamy to wyrażenie do pierwszego równania.
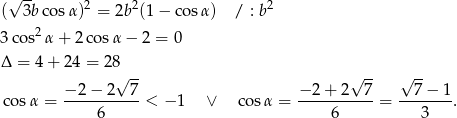
Pierwsze rozwiązanie oczywiście odrzucamy i mamy 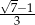 .
.
Sposób II
Podstawiamy wyrażenie na 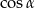 z drugiego równania do pierwszego
z drugiego równania do pierwszego
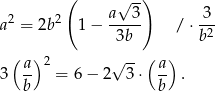
Jeżeli teraz podstawimy 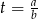 , to mamy zwykłe równanie kwadratowe
, to mamy zwykłe równanie kwadratowe
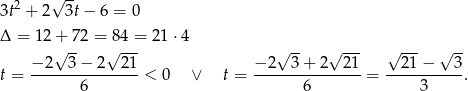
Pierwsze rozwiązanie oczywiście odrzucamy i mamy
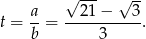
Podstawiamy teraz to wyrażenie do wzoru na 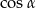 .
.
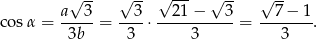
Odpowiedź: