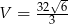Zadanie nr 3724963
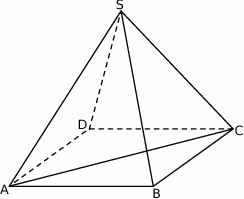
W ostrosłupie prawidłowym czworokątnym 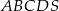 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 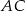 podstawy ma długość
podstawy ma długość 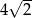 . Kąt
. Kąt 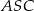 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 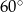 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Dorysujmy wysokość ostrosłupa.
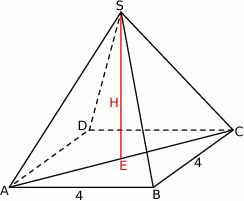
Zauważmy, że trójkąt 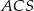 jest trójkątem równoramiennym z kątem między ramionami równym
jest trójkątem równoramiennym z kątem między ramionami równym 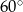 , więc jest trójkąt równoboczny. W takim razie, ze wzoru na wysokość w trójkącie równobocznym, możemy obliczyć wysokość ostrosłupa.
, więc jest trójkąt równoboczny. W takim razie, ze wzoru na wysokość w trójkącie równobocznym, możemy obliczyć wysokość ostrosłupa.
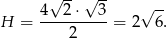
W podstawie ostrosłupa jest kwadrat o boku  i przekątnej długości
i przekątnej długości 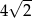 , więc
, więc
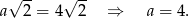
Liczymy objętość ostrosłupa.
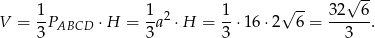
Odpowiedź: