Zadanie nr 2162914
Podstawą ostrosłupa jest kwadrat 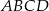 o boku długości 25. Ściany boczne
o boku długości 25. Ściany boczne 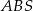 i
i 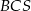 mają takie same pola, każde równe 250. Ściany boczne
mają takie same pola, każde równe 250. Ściany boczne 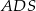 i
i 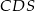 też mają jednakowe pola, każde równe 187,5. Krawędzie boczne
też mają jednakowe pola, każde równe 187,5. Krawędzie boczne 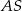 i
i 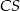 mają równe długości. Oblicz objętość tego ostrosłupa.
mają równe długości. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Szkicujemy ostrosłup – na rysunku zaznaczyliśmy wysokości ścian bocznych: 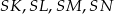 oraz wysokość ostrosłupa
oraz wysokość ostrosłupa 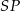 .
.
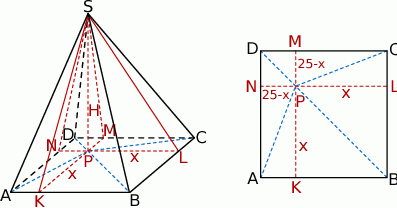
Podane pola ścian bocznych pozwalają nam obliczyć długości wysokości ścian bocznych.
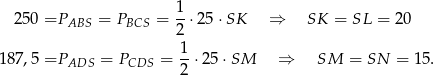
Zauważmy, że równość 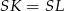 oznacza, że trójkąty prostokątne
oznacza, że trójkąty prostokątne 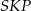 i
i 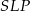 są przystające. Podobnie, z równości
są przystające. Podobnie, z równości 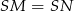 otrzymujemy przystawanie trójkątów prostokątnych
otrzymujemy przystawanie trójkątów prostokątnych 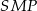 i
i 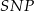 . W szczególności jeżeli oznaczymy
. W szczególności jeżeli oznaczymy 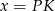 , to
, to 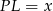 i
i 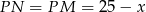 . Aby obliczyć
. Aby obliczyć  piszemy twierdzenia Pitagorasa w trójkątach
piszemy twierdzenia Pitagorasa w trójkątach 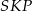 i
i 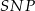 .
.
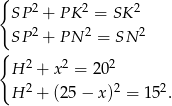
Odejmujemy od pierwszego równania drugie (żeby skrócić 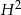 ) i mamy
) i mamy
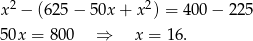
Patrzymy teraz raz jeszcze na pierwsze równanie układu i obliczamy z niego wysokość ostrosłupa.
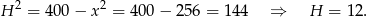
Pozostało obliczyć objętość ostrosłupa.
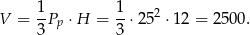
Odpowiedź: 2500

