Zadanie nr 6499183
Podstawą ostrosłupa 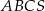 jest trójkąt równoramienny
jest trójkąt równoramienny 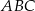 , w którym
, w którym 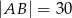 ,
, 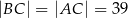 . Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka
. Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka 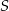 ma długość 26. Oblicz objętość tego ostrosłupa.
ma długość 26. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
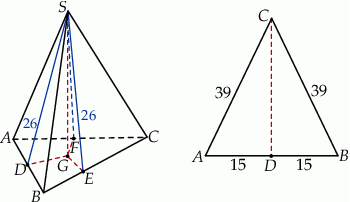
Niech 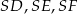 będą wysokościami ścian bocznych, a
będą wysokościami ścian bocznych, a 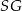 niech będzie wysokością ostrosłupa. Zauważmy, że płaszczyzna
niech będzie wysokością ostrosłupa. Zauważmy, że płaszczyzna 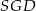 zawiera dwa odcinki (
zawiera dwa odcinki (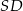 i
i 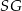 ) prostopadłe do prostej
) prostopadłe do prostej 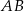 , więc jest prostopadła do tej prostej. W szczególności odcinek
, więc jest prostopadła do tej prostej. W szczególności odcinek 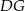 jest prostopadły do
jest prostopadły do 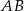 . Analogicznie uzasadniamy, że odcinki
. Analogicznie uzasadniamy, że odcinki 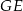 i
i 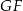 są prostopadłe odpowiednio do
są prostopadłe odpowiednio do 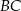 i
i 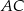 .
.
Zauważmy ponadto, że trójkąty 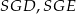 i
i 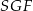 są przystające (bo są prostokątne i mają dwa boki tej samej długości). To oznacza, że
są przystające (bo są prostokątne i mają dwa boki tej samej długości). To oznacza, że 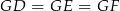 , czyli
, czyli 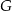 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 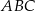 oraz
oraz 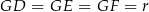 , gdzie
, gdzie  promień okręgu wpisanego w podstawę ostrosłupa.
promień okręgu wpisanego w podstawę ostrosłupa.
Aby obliczyć  potrzebujemy obliczyć pole trójkąta
potrzebujemy obliczyć pole trójkąta 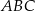 . Liczymy.
. Liczymy.
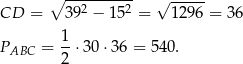
Obliczamy promień okręgu wpisanego.
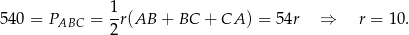
Teraz możemy obliczyć długość wysokości 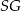 ostrosłupa.
ostrosłupa.
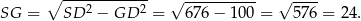
Liczymy objętość ostrosłupa.
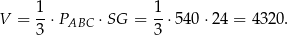
Odpowiedź: 4320

